
【题目】如图1,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,以
的中点,以![]() 为折痕,将
为折痕,将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() ,如图2.
,如图2.
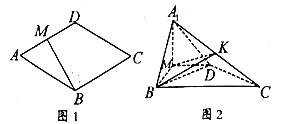
(1)求证:![]() ;
;
(2)若![]() 为
为![]() 的中点,求四面体
的中点,求四面体![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场从2018年1月份起的前这个月,顾客对某商品的需求总量,![]() (单位:件)与x的关系近似地满足
(单位:件)与x的关系近似地满足![]() (其中
(其中![]() ,且
,且![]() ),该商品第x月的进货单价
),该商品第x月的进货单价![]() (单位:元)与x的近似关系是
(单位:元)与x的近似关系是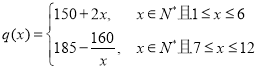 .
.
(1)写出2018年第x月的需求量![]() (单位:件)与x的函数关系式;
(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2018年第几个月销售该商品的月利润![]() 最大,最大月利润为多少元?
最大,最大月利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项均为正数,Sn是数列
各项均为正数,Sn是数列![]() 的前n项的和,对任意的
的前n项的和,对任意的![]() ,都有
,都有![]() .数列
.数列![]() 各项都是正整数,
各项都是正整数,![]() ,且数列
,且数列![]() 是等比数列.
是等比数列.
(1) 证明:数列![]() 是等差数列;
是等差数列;
(2) 求数列![]() 的通项公式
的通项公式![]() ;
;
(3)求满足![]() 的最小正整数n.
的最小正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为![]() (
(![]() ,
,![]() 为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=![]() 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当![]() =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当![]() =
=![]() 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当![]() =
=![]() 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当![]() =-
=-![]() 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面相交于
所在平面相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点, ![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点,
的点, ![]() .
.
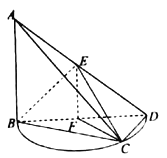
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 为半圆弧
为半圆弧![]() 上的一个三等分点(靠近点
上的一个三等分点(靠近点![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com