
给出四个等式:




(1)写出第 个等式,并猜测第
个等式,并猜测第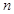 (
(
 )个等式;
)个等式;
(2)用数学归纳法证明你猜测的等式.
(1)第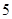 个等式:
个等式: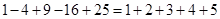 ,第
,第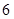 个等式:
个等式: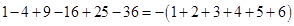 ,第
,第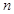 个等式:
个等式: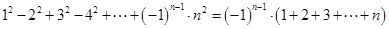 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)通过观察前4个等式的特征不难得到第 个等式,同过归纳,也易猜测第
个等式,同过归纳,也易猜测第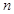 (
(
 )个等式、不过这里涉及到正负号问题,这个问题经常通过
)个等式、不过这里涉及到正负号问题,这个问题经常通过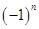 或
或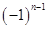 来调控;(2)首先要掌握好数学归纳法证题的规范、完整的证题步骤,而真正的难点和重点是由假设来推导第
来调控;(2)首先要掌握好数学归纳法证题的规范、完整的证题步骤,而真正的难点和重点是由假设来推导第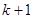 步,这里要充分地利用假设,对于恒等式的证明在利用了假设以后就很容易推导出第
步,这里要充分地利用假设,对于恒等式的证明在利用了假设以后就很容易推导出第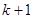 步,如何利用假设呢?就是要创造假设所具备的条件,那才会有假设所具有的结论,故有“凑假设”一说.
步,如何利用假设呢?就是要创造假设所具备的条件,那才会有假设所具有的结论,故有“凑假设”一说.
试题解析:(1)第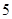 个等式:
个等式: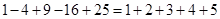 2分
2分
第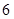 个等式:
个等式: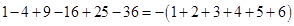 4分
4分
第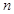 个等式:
个等式: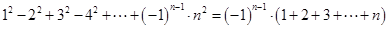 6分
6分
(2)证明:(1)当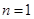 时,左边
时,左边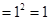 , 右边
, 右边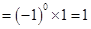 ,左边
,左边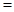 右边,等式成立. 8分
右边,等式成立. 8分
(2)假设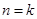 (
(
 )时,等式成立,即
)时,等式成立,即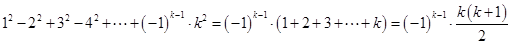 .
.
那么当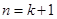 时,
时,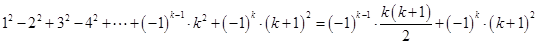
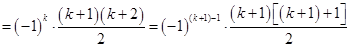
∴当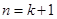 时,等式也成立.
时,等式也成立.
根据(1)、(2)可知,对于任何
 等式均成立. 14分
等式均成立. 14分
考点:1.归纳推理;2. 数学归纳法的应用之一:归纳、猜想和证明.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
在平面几何里,有:“若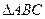 的三边长分别为
的三边长分别为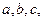 内切圆半径为
内切圆半径为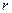 ,则三角形面积为
,则三角形面积为 ”,拓展到空间,类比上述结论,“若四面体
”,拓展到空间,类比上述结论,“若四面体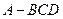 的四个面的面积分别为
的四个面的面积分别为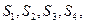 内切球的半径为
内切球的半径为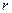 ,则四面体的体积为 ”
,则四面体的体积为 ”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com