
设数列{an}的各项均为正数,前n项和为Sn,已知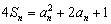 (n∈N*).
(n∈N*).
(1)证明{an}是等差数列,并求an;
(2)设m、k、p∈N*,m+p=2k,求证: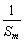 +
+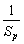 ≥
≥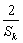 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
解:(1)∵  ,
,
∴ 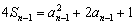 (n≥2).
(n≥2).
两式相减得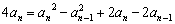 .
.
整理得 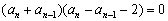 ,
,
∵ 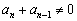 ,
,
∴ 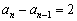 (常数).
(常数).
∴ {an}是以2为公差的等差数列.
又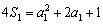 ,即
,即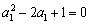 ,解得
,解得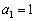 ,
,
∴ an=1+(n-1)×2=2n-1.………………………………………………………4分
(2)由(1)知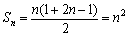 ,∴
Sm=m2,Sp=p2,Sk=k2.
,∴
Sm=m2,Sp=p2,Sk=k2.
由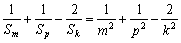
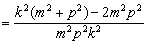
≥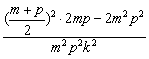 ≥
≥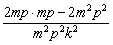 =0,
=0,
即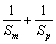 ≥
≥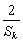 .
………………………………………………………………7分
.
………………………………………………………………7分
(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则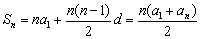 ,
,
∵ 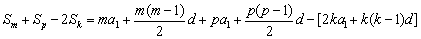
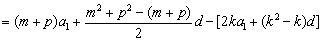 ,
,
把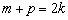 代入上式化简得
代入上式化简得
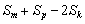 =
=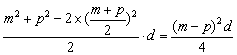 ≥0,
≥0,
∴ Sm+Sp≥2Sk.
又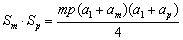 =
=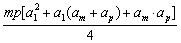
≤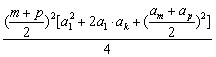
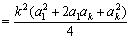
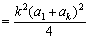
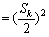 ,
,
∴ 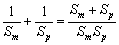 ≥
≥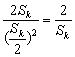 .
.
故原不等式得证.………………………………………………………………14分


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| an+1 |
| an |
| an |
| an+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2a2m(1+S2n) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com