
分析 设AB的中点为D,连接CD,C′D,设平面ABC与平面α所成的角为θ,求出S△CDC′,证明AB⊥平面CDC′,则VC-ABC′=$\frac{1}{3}{S}_{△CDC′}•AB$=$\frac{1}{2}$sin2θ,从而得出体积的最大值.
解答 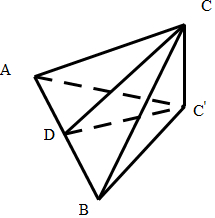 解:设AB的中点为D,连接CD,C′D,
解:设AB的中点为D,连接CD,C′D,
∵△ABC是边长为2的等边三角形,∴AB⊥CD,CD=$\sqrt{3}$.
∵CC′⊥α,AB?α,
∴CC′⊥AB,又CD∩CC′=C,
∴AB⊥平面CDC′,
∴∠CDC′为平面ABC与平面α所成的角,
设∠CDC′=θ,则CC′=CDsinθ=$\sqrt{3}$sinθ,C′D=$\sqrt{3}$cosθ,
∴S△CDC′=$\frac{1}{2}CD•C′D$=$\frac{3}{2}$sinθcosθ=$\frac{3}{4}$sin2θ,
∴VC-ABC′=$\frac{1}{3}{S}_{△CDC′}•AB$=$\frac{1}{3}×\frac{3}{4}sin2θ×2$=$\frac{1}{2}$sin2θ,
∴当2θ=$\frac{π}{2}$即$θ=\frac{π}{4}$时,V取得最大值$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了项目垂直的判定,棱锥的体积计算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {∅,{3}} | C. | {∅} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
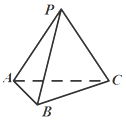 如图,在三棱锥P-ABC中,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°.
如图,在三棱锥P-ABC中,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(-∞,-1)上单调递增 | |
| B. | 函数f(x)在(-∞,-1)上单调递减 | |
| C. | 若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 | |
| D. | 若b=0,则函数f(x)的图象与直线y=10只有一个公共点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{x^2}$,$g(x)={(\sqrt{x})^2}$ | B. | f(x)=2log2x,$g(x)={log_2}{x^2}$ | ||
| C. | f(x)=ln(x-1)-ln(x+1),$g(x)=ln(\frac{x-1}{x+1})$ | D. | f(x)=lg(1-x)+lg(1+x),g(x)=lg(1-x2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com