分析:(I)当M在A1C1中点时,BC1∥平面MB1A.连接NB1并延长与CB延长线交于G,在△CGN中,利用BC1为中位线得BC1∥GN,从而可证BC1∥平面MAB1;
(II)可证∠MAC为平面MB1A与平面ABC所成二面角的平面角,进而可求;
(Ⅲ)设动点M到平面A1ABB1的距离为hM,利用等体积进行转化,从而可求B-AB1M体积最大值.
解答:
解:(I)当M在A
1C
1中点时,BC
1∥平面MB
1A
∵M为A
1C
1中点,延长AM、CC
1,使AM与CC
1延长线交于N,则NC
1=C
1C=a
连接NB
1并延长与CB延长线交于G,则BG=CB,NB
1=B
1G (2分)
在△CGN中,BC
1为中位BC
1∥GN
又GN?平面MAB
1,∴BC
1∥平面MAB
1 (4分)
(II)∵△AGC中,BC=BA=BG∴∠GAC=90°
即AC⊥AG 又AG⊥AA
1 AA
1∩AC=A∴AG⊥平面A
1ACC
1,AG⊥AM(6分)
∴∠MAC为平面MB
1A与平面ABC所成二面角的平面角∴
tan∠MAC==2∴所求二面角为 arctan2.(8分)
(Ⅲ)设动点M到平面A
1ABB
1的距离为h
M.
VB-AB1M=VM-AB1B=S△ABB1•hM=•a2hM≤a2•a=a3即B-AB
1M体积最大值为
a3.此时M点与C
1重合. (12分)
点评:本题以正三棱柱为载体,考查线面平行,考查面面角,同时考查了几何体的体积,综合性强.

 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点. 解:(I)当M在A1C1中点时,BC1∥平面MB1A
解:(I)当M在A1C1中点时,BC1∥平面MB1A

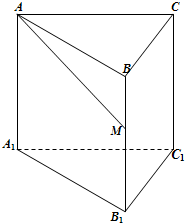 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.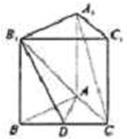 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.