
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)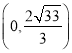
【解析】试题分析:(1)抛物线的焦点到准线的距离为![]() 可得
可得![]() ,从而得到抛物线的方程,然后设出切线切线
,从而得到抛物线的方程,然后设出切线切线![]() 的方程为
的方程为![]() ,由
,由![]() 求得
求得![]() ,由切点在抛物线上可得到
,由切点在抛物线上可得到![]() ,即为所求。(2)由(1)得到以线段
,即为所求。(2)由(1)得到以线段![]() 为直径的圆为圆
为直径的圆为圆![]() 。由题意只需考虑斜率为正数的直线
。由题意只需考虑斜率为正数的直线![]() 即可,根据几何知识得
即可,根据几何知识得![]() ,故
,故![]() 的方程为
的方程为![]() ,由弦长公式可得
,由弦长公式可得![]() ,又
,又![]() ,所以
,所以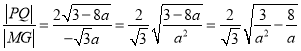 ,最后根据
,最后根据![]() 可得
可得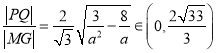 。
。
试题解析:
(1)由抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,得
,得![]() ,
,
则抛物线![]() 的方程为
的方程为![]() .
.
设切线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,
当![]() 时,点
时,点![]() 的横坐标为
的横坐标为![]() ,
,
则![]() ,
,
当![]() 时,同理可得
时,同理可得![]() .
.
综上得![]() 。
。
(2)由(1)知, ![]() ,
,
所以以线段![]() 为直径的圆为圆
为直径的圆为圆![]() ,
,
根据对称性,只要探讨斜率为正数的直线![]() 即可,
即可,
因为![]() 为直线
为直线![]() 与圆
与圆![]() 的切点,
的切点,
所以![]() ,
, ![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
由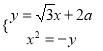 消去
消去![]() 整理得
整理得![]() ,
,
因为直线与圆相交,所以![]() 。
。
设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以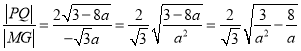 ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以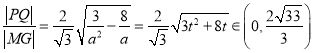 .
.


科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 做直线
做直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘车补贴标准如下表:

某校研究性学习小组,从汽车市场上随机选取了![]() 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程![]() (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:

(1)求![]() 的值;
的值;
(2)若从这![]() 辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
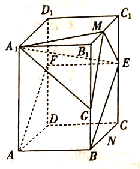
【题目】如图,四边形![]() 是正四棱柱
是正四棱柱![]() 的一个截面,此截面与棱
的一个截面,此截面与棱![]() 交于点
交于点![]() ,
, ![]() ,其中
,其中![]() 分别为棱
分别为棱![]() 上一点.
上一点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,若四面体
上一点,若四面体![]() 与四棱锥
与四棱锥![]() 的体积相等,求
的体积相等,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C(t,![]() ) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y﹣4=0与圆C交于点M、N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x)在(﹣∞,0]上单调递减,则不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com