
 ,0)与定直线l1:x=
,0)与定直线l1:x= 的距离之比为常数
的距离之比为常数 .
. )引曲线C的弦AB恰好被点Q平分,求弦AB所在的直线方程;
)引曲线C的弦AB恰好被点Q平分,求弦AB所在的直线方程; 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程.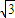 ,0)与定直线l1:x=
,0)与定直线l1:x=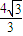 的距离之比为常数
的距离之比为常数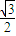 ,建立方程,化简,即可得到椭圆的标准方程;
,建立方程,化简,即可得到椭圆的标准方程; =k(x-1)代入椭圆方程,消去y可得一元二次方程,利用过点Q(1,
=k(x-1)代入椭圆方程,消去y可得一元二次方程,利用过点Q(1, )引曲线C的弦AB恰好被点Q平分,即可求直线的斜率,从而可得直线的方程;
)引曲线C的弦AB恰好被点Q平分,即可求直线的斜率,从而可得直线的方程;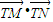 ,利用配方法,确定最小值为-
,利用配方法,确定最小值为-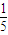 ,可得M的坐标,从而可求圆T的方程.
,可得M的坐标,从而可求圆T的方程.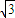 ,0)与定直线l1:x=
,0)与定直线l1:x=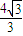 的距离之比为常数
的距离之比为常数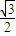 .
. ;
;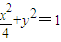 .
. =k(x-1)代入椭圆方程,消去y可得(1+4k2)x2-4k(2k-1)x+(1-2k)2-4=0
=k(x-1)代入椭圆方程,消去y可得(1+4k2)x2-4k(2k-1)x+(1-2k)2-4=0 )引曲线C的弦AB恰好被点Q平分,所以
)引曲线C的弦AB恰好被点Q平分,所以 ,解得k=-
,解得k=- .
. =
=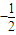 (x-1),即l:y=
(x-1),即l:y=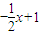 .
.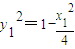 .
. ,
,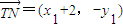 ,
,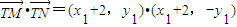 =
=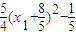 .
.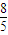 时,
时,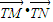 取得最小值为-
取得最小值为-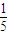 .
. ,故M(-
,故M(-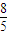 ,
,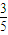 ),又点M在圆T上,代入圆的方程得到
),又点M在圆T上,代入圆的方程得到 .
.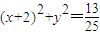 .
.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
| PQ |
| RS |
| AB |
| AF |
| TB |
| FT |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| TM |
| TN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| TM |
| TN |
查看答案和解析>>
科目:高中数学 来源:2012-2013学江苏省无锡市青阳高级中学高三(上)月考数学试卷(一)(解析版) 题型:解答题
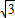 ,0)与定直线l1:x=
,0)与定直线l1:x=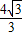 的距离之比为常数
的距离之比为常数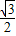 .
. •
• 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com