
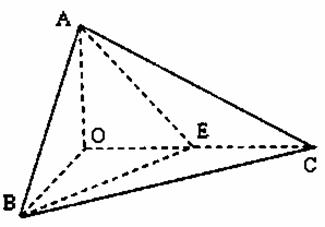
如图,已知三棱锥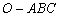 的侧棱
的侧棱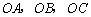 两两垂直,
两两垂直,
且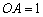 ,
,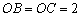 ,
,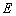 是
是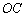 的中点。
的中点。
(1)求异面直线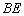 与
与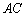 所成角的余弦值;
所成角的余弦值;
(2)求直线BE和平面 的所成角的正弦值。
的所成角的正弦值。
科目:高中数学 来源: 题型:
设有以下两个程序:
程序(1) A=-8 程序(2) x=1/4
B=2 i=1
If A<0 then while i<3
A=-A x=1/(1+x)
END if i=i+1
B=B^2 wend
A=A+B print x
C=A-2*B end
A=A/C
B=B*C+1
Print A,B,C
程序(1)的输出结果是______,________,_________.
程序(2)的输出结果是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
①一个命题的逆命题为真,它的否命题也一定为真;
②在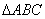 中,“
中,“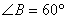 ”是“
”是“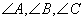 三个角成等差数列”的充要条件.
三个角成等差数列”的充要条件.
③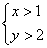 是
是 的充要条件;④“am2<bm2 ”是“a<b”的充分必要条件.
的充要条件;④“am2<bm2 ”是“a<b”的充分必要条件.
以上说法中,判断错误的有___________..
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点F1、F2分别是椭圆 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率 为 ( )
为 ( )
(A)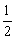 (B)
(B) 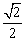 (C)
(C)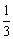 (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
如果命题“p或q”是真命题,“非p”是假命题,那么( )
A.命题p一定是假命题 B.命题q一定是假命题
C.命题q一定是真命题 D.命题q是真命题或者假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com