
| A. | |m|>|n| | B. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | C. | sinm>sinn | D. | m${\;}^{\frac{1}{2}}$>n${\;}^{\frac{1}{2}}$ |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
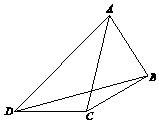 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 事件A发生的概率P(A)是0<P(A)<1 | |
| B. | 事件A发生的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计有明显疗效的可能性为76% | |
| D. | 某奖券中奖率为0.5,则某人购买此券10张,一定有5张中奖 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p或q”为真,“非q”为假 | B. | “p且q”为假,“非p”为假 | ||
| C. | “p且q”为假,“非p”为真 | D. | “p且q”为假,“p或q”为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com