
(本题满分12分)
如图,四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。
(1)求证:CD⊥AE;
(2)求证:PD⊥面ABE。
(1)要证明线线垂直,则只要根据线面垂直的性质定理可以证明。
(2)对于线面垂直的证明,一般先证明线线垂直,然后结合线面垂直的判定定理得到,关键是证明AE⊥PD和BA⊥PD。
解析试题分析:(I)证明:∵PA⊥底面ABCD
∴CD⊥PA
又CD⊥AC,PA∩AC=A,
故CD⊥面PAC
AE 面PAC,故CD⊥AE
面PAC,故CD⊥AE
(II)证明:PA=AB=BC,∠ABC=60°,
故PA=ACE是PC的中点,故AE⊥PC
由(I)知CD⊥AE,从而AE⊥面PCD,
故AE⊥PD
易知BA⊥PD,故PD⊥面ABE
考点:线线垂直和线面垂直
点评:本试题考查了空间中线线与线面的位置关系的运用,关键是熟练的结合线线与线面垂直的判定定理和性质定理来得到证明,属于基础题。


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
如图,在梯形△ABCD中,AB//CD,AD=DC-=CB=1, ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.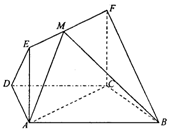
(1)求证:BC⊥平面ACFE;
(2)若M为线段EF的中点,设平面MAB与平面FCB所成角为 ,求
,求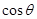 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四边形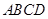 中,
中, 为正三角形,
为正三角形, ,
,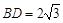 ,
, 与
与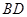 交于
交于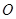 点.将
点.将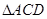 沿边
沿边 折起,使
折起,使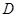 点至
点至 点,已知
点,已知 与平面
与平面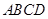 所成的角为
所成的角为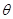 ,且
,且 点在平面
点在平面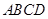 内的射影落在
内的射影落在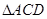 内.
内.
(Ⅰ)求证: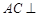 平面
平面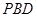 ;
;
(Ⅱ)若已知二面角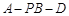 的余弦值为
的余弦值为 ,求
,求 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示在四棱锥P—ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形。(12分)
(1)求PC和平面ABCD所成角的大小;
(2)求二面角B─AC─P的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足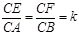 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 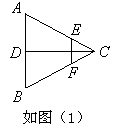
(Ⅰ) 求二面角B-AC-D的大小;
(Ⅱ) 若异面直线AB与DE所成角的余弦值为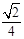 ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,矩形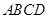 所在平面与平面
所在平面与平面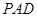 垂直,
垂直,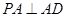 ,且
,且 ,
, 为
为 上的动点.
上的动点.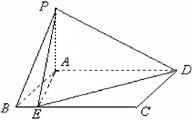
(Ⅰ)当 为
为 的中点时,求证:
的中点时,求证: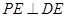 ;
;
(Ⅱ)若 ,在线段
,在线段 上是否存在点E,使得二面角
上是否存在点E,使得二面角 的大小为
的大小为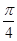 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com