Question

20．已知任意两个向量$\overrightarrow{a}$，$\overrightarrow{b}$，不等式|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|是否正确？为什么？

Answer 1

分析 可讨论向量$\overrightarrow{a}，\overrightarrow{b}$是否共线，然后根据向量加法的三角形法则和平行四边形法则作出向量$\overrightarrow{a}+\overrightarrow{b}$，由图形即可判断$|\overrightarrow{a}+\overrightarrow{b}|$和$|\overrightarrow{a}|+|\overrightarrow{b}|$的大小关系，从而判断出不等式$|\overrightarrow{a}|+|\overrightarrow{b}|≤|\overrightarrow{a}|+|\overrightarrow{b}|$是否正确．

解答 解：（1）当向量$\overrightarrow{a}，\overrightarrow{b}$共线，且方向相同时，$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}|+|\overrightarrow{b}|$，如图所示：

（2）当向量$\overrightarrow{a}，\overrightarrow{b}$共线，且方向相反时，$|\overrightarrow{a}+\overrightarrow{b}|＜|\overrightarrow{a}|+|\overrightarrow{b}|$，如图所示：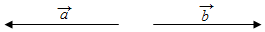

（3）当向量$\overrightarrow{a}，\overrightarrow{b}$不共线时，设$\overrightarrow{OA}=\overrightarrow{a}，\overrightarrow{OB}=\overrightarrow{b}$，如图，作$\overrightarrow{OC}=\overrightarrow{a}+\overrightarrow{b}$：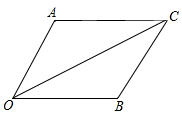

根据两边之和大于第三边得：$|\overrightarrow{a}+\overrightarrow{b}|＜|\overrightarrow{a}|+|\overrightarrow{b}|$；
∴综上得，不等式$|\overrightarrow{a}+\overrightarrow{b}|≤|\overrightarrow{a}|+|\overrightarrow{b}|$正确．

点评 考查向量加法的三角形法则和平行四边形法则，以及三角形的两边之和大于第三边定理．