
 :
: 的离心率为
的离心率为 ,左焦点为
,左焦点为 .
.  的方程;
的方程; 与曲线
与曲线 交于不同的
交于不同的 、
、 两点,且线段
两点,且线段 的中点
的中点 在圆
在圆 上,求
上,求 的值.
的值.科目:高中数学 来源:不详 题型:解答题
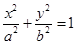 (
( )上任意一点到两焦点距离之和为
)上任意一点到两焦点距离之和为 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,
, ,点
,点 是右准线上任意一点,过
是右准线上任意一点,过 作直 线
作直 线 的垂线
的垂线 交椭圆于
交椭圆于 点.
点.
 的标准方程;
的标准方程; 与直线
与直线 的斜率之积是定值;
的斜率之积是定值; 的纵坐标为3,过
的纵坐标为3,过 作动直线
作动直线 与椭圆交于两个不同点
与椭圆交于两个不同点 ,在线段
,在线段 上取点
上取点 ,满足
,满足 ,试证明点
,试证明点 恒在一定直线上.
恒在一定直线上.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
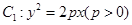 的焦点
的焦点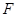 以及椭圆
以及椭圆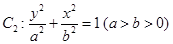 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆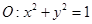 上.
上.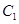 和椭圆
和椭圆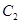 的标准方程;
的标准方程;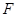 的直线交抛物线
的直线交抛物线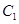 于
于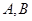 两不同点,交
两不同点,交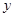 轴于点
轴于点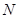 ,已知
,已知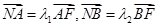 ,则
,则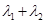
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的离心率为
的离心率为 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为 ,直线
,直线 交椭圆于不同的两点
交椭圆于不同的两点 。
。 到直线
到直线 的距离为
的距离为 ,求
,求 面积的最大值。
面积的最大值。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是双曲线
是双曲线 的两个顶点,点
的两个顶点,点 是双曲线上异于
是双曲线上异于 的一点,连接
的一点,连接 (
( 为坐标原点)交椭圆
为坐标原点)交椭圆 于点
于点 ,如果设直线
,如果设直线 的斜率分别为
的斜率分别为 ,且
,且 ,假设
,假设 ,则
,则 的值为( )
的值为( )| A.1 | B. | C.2 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 年
年 月
月 日
日 时
时 分
分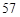 秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约
秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约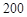 公里、远地点高度约
公里、远地点高度约 万公里的直接奔月椭圆(地球球心
万公里的直接奔月椭圆(地球球心 为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面
为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面 公里、近月面
公里、近月面 公里(月球球心
公里(月球球心 为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以
为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以 为圆心、距月面
为圆心、距月面 公里的圆形轨道Ⅲ绕月飞行,并开展相关技术试验和科学探测。已知地球半径约为
公里的圆形轨道Ⅲ绕月飞行,并开展相关技术试验和科学探测。已知地球半径约为 公里,月球半径约为
公里,月球半径约为 公里。
公里。 为右焦点,求椭圆轨道Ⅱ的标准方程。
为右焦点,求椭圆轨道Ⅱ的标准方程。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com