
分析 先根据抛物线方程求得焦点坐标,根据抛物线的定义可知P到准线的距离等于点P到焦点的距离,进而问题转化为求点P到点Q的距离与点P到抛物线的焦点距离之和的最小值,根据图象可知当P,Q,F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小,为圆心到焦点F的距离减去圆的半径.
解答 解:由于点C为抛物线的焦点,则|PC|等于点P到抛物线准线x=-2的距离d.
又圆心C到抛物线准线的距离为4,
则|PQ|+|PC|=|PQ|+d≥3.当点P为原点,Q为(1,0)时取等号.
故|PQ|+|PC|得最小值为3.
故答案为:3.
点评 本题主要考查了抛物线的应用.考查了学生转化和化归,数形结合等数学思想.属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
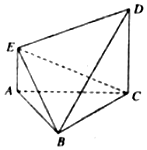 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
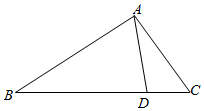 如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC
如图,在△ABC中,角A,B,C所对的边为a,b,c,满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com