
| A. | 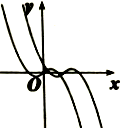 | B. | 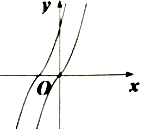 | C. | 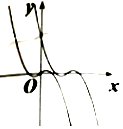 | D. | 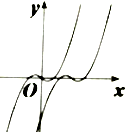 |
分析 去绝对值化简f(x)解析式,对a进行讨论,根据二次函数的性质判断f(x)的单调性,再根据函数平移规律得出两函数图象.
解答 解:f(x)=x(1+a|x|)=x+ax|x|=$\left\{\begin{array}{l}{a{x}^{2}+x,x≥0}\\{-a{x}^{2}+x,x<0}\end{array}\right.$,
(1)若a>0,则当x≥0时,对称轴为x=-$\frac{1}{2a}$<0,开口向上,
x<0时,对称轴为x=$\frac{1}{2a}$>0,开口向下,
∴f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递增,且f(0)=0,
f(x+a)是由f(x)向左平移a的单位得到的,
此时函数图象为B,
(2)若a<0,则当x≥0时,对称轴为x=-$\frac{1}{2a}$>0,开口向下,
x<0时,对称轴为x=$\frac{1}{2a}$<0,开口向上,
∴f(x)在(0,+∞)上先减后增,在(-∞,0)先减后增,且f(0)=0,
f(x+a)是由f(x)向右平移|a|的单位得到的,
此时函数图象为A或C,
故选D.
点评 本题考查了函数的单调性判断,二次函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
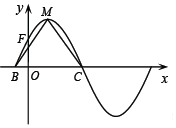 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
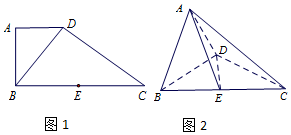 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体查看答案和解析>>
科目:高中数学 来源: 题型:选择题
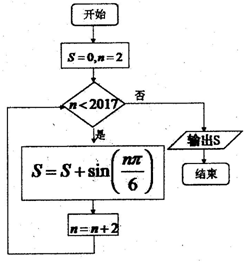
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com