
分析 (Ⅰ)直线l为过定点A(0,1),倾斜角在$[{\frac{π}{2},π})$内的一条直线,圆C的方程为(x-1)2+y2=1,即可讨论直线l与圆C的公共点个数;
(Ⅱ)过极点作直线l的垂线,垂足为P,联立$\left\{\begin{array}{l}ρ=2cosθ\\ ρ=sinθ({0≤θ<\frac{π}{2}})\end{array}\right.$得$ρ=\frac{{2\sqrt{5}}}{5}$,即可求点P的轨迹与圆C相交所得弦长.
解答 解:(Ⅰ)直线l为过定点A(0,1),倾斜角在$[{\frac{π}{2},π})$内的一条直线,
圆C的方程为(x-1)2+y2=1,∴当$α=\frac{π}{2}$时,直线l与圆C有1个公共点;
当$\frac{π}{2}<α<π$时,直线l与圆C有2个公共点
(Ⅱ)依题意,点P在以OA为直径的圆上,可得轨迹极坐标方程为$ρ=sinθ({0≤θ<\frac{π}{2}})$.
联立$\left\{\begin{array}{l}ρ=2cosθ\\ ρ=sinθ({0≤θ<\frac{π}{2}})\end{array}\right.$得$ρ=\frac{{2\sqrt{5}}}{5}$.
∴点P的轨迹与圆C相交所得弦长是$\frac{{2\sqrt{5}}}{5}$.
点评 本题考查极坐标方程的运用,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -$\frac{25}{19}$ | D. | $\frac{25}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
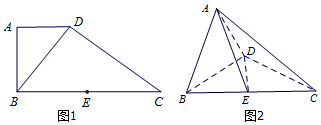 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
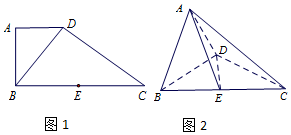 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com