练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，则$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$

    分析 利用两个向量的数量积公式，以及两个向量的夹角公式，求得$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角的余弦值，可得$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角．

    解答 解：∵已知$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$，
    设$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为θ，θ∈[0，π]，
    则cosθ=$\frac{\overrightarrow{a}•（\overrightarrow{a}-\overrightarrow{b}）}{|\overrightarrow{a}|•|\overrightarrow{a}-\overrightarrow{b}|}$=$\frac{{\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}}{1•\sqrt{{（\overrightarrow{a}-\overrightarrow{b}）}^{2}}}$
    =$\frac{1-1•1•cos\frac{π}{3}}{\sqrt{{\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}}$=$\frac{\frac{1}{2}}{\sqrt{1-2•1•1•cos\frac{π}{3}+1}}$=$\frac{1}{2}$，
    ∴θ=$\frac{π}{3}$，
    故选：B．

    点评 本题主要考查用数量积表示两个两个向量的夹角，两个向量的数量积公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．已知直线l的参数方程为$\left\{\begin{array}{l}x=tcosα\\ y=1+tsinα\end{array}\right.$（t为参数，$\frac{π}{2}≤α＜π$），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=2cosθ．
    （Ⅰ）讨论直线l与圆C的公共点个数；
    （Ⅱ）过极点作直线l的垂线，垂足为P，求点P的轨迹与圆C相交所得弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．随着“全面二孩”政策推行，我市将迎来生育高峰，今年新春伊始，各医院产科就已经一片忙碌，至今热度不减，卫生部门进行调查统计，期间发现各医院的新生儿中，不少都是“二孩”，在人民医院，共有50个宝宝降生，其中25个是“二孩”宝宝；博爱医院共有30个宝宝降生，其中10个是“二孩”宝宝．
    （1）根据以上数据，完成下面的2×2列联表，并判断是否有90%的把握认为一孩或二孩宝宝的出生与医院有关？
     一孩二孩合计
    人民医院   
    博爱医院   
    合计   
    （2）从两个医院当前出生的所有宝宝中按分层抽样方法抽取8个宝宝做健康咨询，若从这8个宝宝抽取两个宝宝进行体检．求这两个宝宝恰好都是来自人民医院的概率．
    附：${K^2}=\frac{{n{{（{αb-bc}）}^2}}}{{（{α+b}）（{c+d}）（{α+c}）（{b+d}）}}$
    P（k2＞k0）0.40.250.150.10
    k00.7081.3232.0722.706

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．执行如图的程序框图，输出的结果为（　　）
    A．136B．134C．268D．266

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

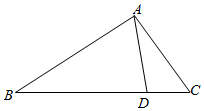    1．如图，在△ABC中，角A，B，C所对的边为a，b，c，满足sin2A+sin2C-sin2B=$\sqrt{3}$sinA•sinC
    （Ⅰ）求角B；
    （Ⅱ）点D在线段BC上，满足DA=DC，且a=11，cos（A-C）=$\frac{\sqrt{5}}{5}$，求线段DC的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．数列{an}满足a1=-1，an+1+2an=3．
    （Ⅰ）证明{an-1}是等比数列，并求数列{an}通项公式；
    （Ⅱ）已知符号函数sgn（x）=$\left\{\begin{array}{l}{1，x＞0}\\{0，x=0}\\{-1，x＜0}\end{array}\right.$，设bn=an•sgn{an}，求数列{bn}的前100项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知一个圆锥底面半径为1，母线长为3，则该圆锥内切球的表面积为（　　）
    A．πB．$\frac{3π}{2}$C．2πD．3π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

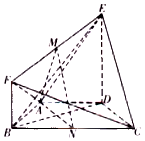    15．在如图所示的几何体ABCDEF中，四边形ABCD是等腰梯形，AD∥BC，∠ABC=60°，AB=$\frac{1}{2}$BC=1，DE⊥平面ABCD，BF∥DE，DE=2BF，M，N分别是EF、BC的中点．
    （1）求证：BD⊥平面MAN；
    （2）已知直线BE与平面ABCD所成的角为45°，求二面角A-BE-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设数列{an}满足a1=2，a2=6，且an+2-2an+1+an=2，用[x]表示不超过x的最大整数，如[0.6]=0，[1.2]=1，则$[{\frac{m}{a_1}+\frac{m}{a_2}+…+\frac{m}{a_m}}]$的值用m表示为m-1．

    查看答案和解析>>

    同步练习册答案