
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
分析 (1)计算K2,与2.072比较大小得出结论.
(2)从两个医院当前出生的所有宝宝中按分层抽样方法抽取8个宝宝做健康咨询,人民医院5人,博爱医院3人,确定基本事件的情况,即可求出概率.
解答 解:(1)
| 一孩 | 二孩 | 合计 | |
| 人民医院 | 25 | 25 | 50 |
| 博爱医院 | 20 | 10 | 30 |
| 合计 | 45 | 35 | 80 |
点评 本题考查了分层抽样原理,古典概型的概率计算,独立检验的统计思想,属于基础题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
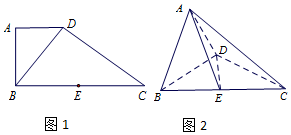 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体查看答案和解析>>
科目:高中数学 来源: 题型:选择题
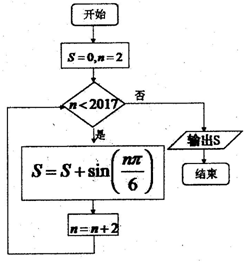
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com