
| A. | 2 | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
分析 确定△QAP为等边三角形,设AQ=2R,则OP=$\frac{1}{2}$R,利用勾股定理,结合余弦定理和离心率公式,计算即可得出结论.
解答 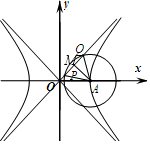 解:因为∠PAQ=60°且$\overrightarrow{OQ}=5\overrightarrow{OP}$,
解:因为∠PAQ=60°且$\overrightarrow{OQ}=5\overrightarrow{OP}$,
所以△QAP为等边三角形,
设AQ=2R,则PQ=2R,OP=$\frac{1}{2}$R,
渐近线方程为y=$\frac{b}{a}$x,A(a,0),
取PQ的中点M,则AM=$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$,
由勾股定理可得(2R)2-R2=($\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$)2,
所以(ab)2=3R2(a2+b2)①,
在△OQA中,$\frac{(\frac{5}{2}R)^{2}+(2R)^{2}-{a}^{2}}{2•\frac{5}{2}R•2R}$=$\frac{1}{2}$,
所以$\frac{21}{4}$R2=a2②
①②结合c2=a2+b2,
解得c2=$\frac{7}{4}$b2=$\frac{7}{4}$(c2-a2),
即为3c2=7a2,
可得e=$\frac{c}{a}$=$\sqrt{\frac{7}{3}}$=$\frac{\sqrt{21}}{3}$.
故选:B.
点评 本题考查双曲线的性质:离心率,考查余弦定理、勾股定理,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2-i | B. | 2-i | C. | $1-\sqrt{2}i$ | D. | $-1-\sqrt{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 周一 | 无雨 | 无雨 | 有雨 | 有雨 |
| 周二 | 无雨 | 有雨 | 无雨 | 有雨 |
| 收益 | 10万元 | 8万元 | 5万元 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$-$\frac{1}{2}$i | B. | -$\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com