
分析 由函数f(x)=ln$\frac{1-x}{1+x}$=ln($\frac{2}{1+x}-1$),根据函数的各性质依次判断各选项即可.
解答 解:函数f(x)=ln$\frac{1-x}{1+x}$=ln($\frac{2}{1+x}-1$),
其定义域满足:(1-x)(1+x)>0,解得:-1<x<1,∴定义域为{x|-1<x<1}.∴①不对.
由f(-x)=ln$\frac{1-x}{1+x}$=ln$\frac{1+x}{1-x}$=ln($\frac{1-x}{1+x}$)-1=-ln$\frac{1-x}{1+x}$=-f(x),是奇函数,∴②对.
定义域为{x|-1<x<1}.函数y=$\frac{2}{1+x}-1$在定义内是减函数,根据复合函数的单调性,同增异减,∴f(x)在定义域上是减函数;③不对.
f(x1)+f(x2)=ln$\frac{1-{x}_{1}}{1+{x}_{1}}$+ln$\frac{1-{x}_{2}}{1+{x}_{2}}$=ln($\frac{1-{x}_{1}}{1+{x}_{1}}$×$\frac{1-{x}_{2}}{1+{x}_{2}}$)=f($\frac{{x}_{1}+{x}_{2}}{1+{x}_{1}{x}_{2}}$).∴④对.
故答案为②④
点评 本题考查了对数函数的各性质判断和运用.属于中档题


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
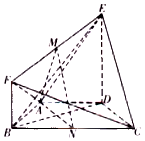 在如图所示的几何体ABCDEF中,四边形ABCD是等腰梯形,AD∥BC,∠ABC=60°,AB=$\frac{1}{2}$BC=1,DE⊥平面ABCD,BF∥DE,DE=2BF,M,N分别是EF、BC的中点.
在如图所示的几何体ABCDEF中,四边形ABCD是等腰梯形,AD∥BC,∠ABC=60°,AB=$\frac{1}{2}$BC=1,DE⊥平面ABCD,BF∥DE,DE=2BF,M,N分别是EF、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
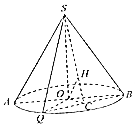 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$-$\frac{1}{2}$i | B. | -$\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com