
(本题10分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.

(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
(Ⅰ)见解析;(Ⅱ)cos∠MNO= =
= 。
。
【解析】(I) 取AC的中点O,连接DO,则DO⊥AC,因为平面ACD⊥平面ABC,所以DO⊥平面ABC,∴DO⊥BC,可得易证: ,从而可证出BC⊥平面ACD;
,从而可证出BC⊥平面ACD;
(II)找(或做)出二面角的平面角.取CD的中点N,连接MO, NO, MN,则MO∥BC,
∴MO⊥平面ACD,∴MO⊥CD,∵AD⊥CD,ON∥AD,∴ON⊥CD,又∵MO∩NO=O,
∴CD⊥平面MON,∴CD⊥MN,∴∠MNO是所求二面角的平面角.

解:(Ⅰ)取AC的中点O,连接DO,则DO⊥AC,
∵平面ADC⊥平面ABC,∴DO⊥平面ABC,∴DO⊥BC,………2分
在直角梯形ABCD中,连接CM,可得CM=AD=2,AC=BC=2 ,
,
∴AC2+BC2=AB2,∴AC⊥BC,
又∵DO∩AC=O,∴BC⊥平面ACD;………………………………3分
(Ⅱ)取CD的中点N,连接MO, NO, MN,
则MO∥BC,∴MO⊥平面ACD,∴MO⊥CD,……………………1分
∵AD⊥CD,ON∥AD,∴ON⊥CD,又∵MO∩NO=O,
∴CD⊥平面MON,∴CD⊥MN,∴∠MNO是所求二面角的平面角…2分
在Rt△MON中,MO= =
= ,NO=
,NO= =1,
=1,
∴MN= =
= ,∴cos∠MNO=
,∴cos∠MNO= =
= ………………2分
………………2分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012年山东省济宁市高二上学期期中考试文科数学 题型:解答题
(本题10分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上
(Ⅰ)求AB边上的高CE所在直线的方程
(Ⅱ)求△ABC的面积
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高一上学期期中考试数学试卷 题型:解答题
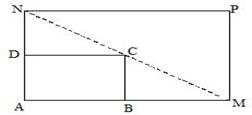
(本题10分)如图所示,将一矩形花坛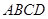 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛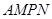 ,要求
,要求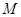 在
在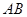 的延长线上,
的延长线上,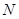 在
在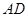 的延长线上,且对角线
的延长线上,且对角线 过
过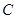 点.已知
点.已知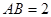 米,
米,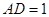 米.
米.
(1)设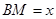 (单位:米),要使花坛
(单位:米),要使花坛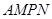 的面积大于9平方米,求
的面积大于9平方米,求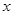 的取值范围;
的取值范围;
(2)若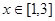 (单位:米),则当
(单位:米),则当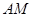 ,
,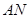 的长度分别是多少时,花坛
的长度分别是多少时,花坛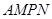 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源:2012届辽宁省抚顺市六校联合体高二下学期期末考试数学 题型:解答题
请考生在(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。
(本题10分)
 如图,
如图, 内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且
内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且
(Ⅰ)求证: 
(Ⅱ)如果 ,⊙O的半径为1,
,⊙O的半径为1,
且 为弧
为弧 的中点,求
的中点,求 的长。
的长。
查看答案和解析>>
科目:高中数学 来源:2012届温州十校联合体高二第一学期期末联考数学试卷(理科) 题型:解答题
本题10分)如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16 m., 为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
(1)一条船船顶部宽4m,要使这艘船安全通过,则船在水面以上部分高不能超过多少米?
(2)近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞. 试问:一艘顶部宽 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com