
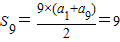 ,解a1+a9=2,利用性质可得a4+a6=a1+a9=2
,解a1+a9=2,利用性质可得a4+a6=a1+a9=2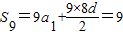 ,解得a1+4d=1,而a4+a6=2(a1+4d)=2
,解得a1+4d=1,而a4+a6=2(a1+4d)=2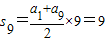
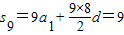 ⇒a1+4d=1
⇒a1+4d=1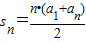 ,整体代入可求a1+a9的值,然后运用等差数列的性质m+n=p+q,则an+am=ap+aq;(法二)利用等差数列的和公式
,整体代入可求a1+a9的值,然后运用等差数列的性质m+n=p+q,则an+am=ap+aq;(法二)利用等差数列的和公式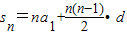 ,利用整体思想求解
,利用整体思想求解 

 智慧小复习系列答案
智慧小复习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com