
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
【答案】D
【解析】解:由于f(n)=sin ![]() 的周期T=50
的周期T=50
由正弦函数性质可知,a1 , a2 , …,a24>0,a25=0,a26 , a27 , …,a49<0,a50=0
且sin ![]() ,sin
,sin ![]() …但是f(n)=
…但是f(n)= ![]() 单调递减
单调递减
a26…a49都为负数,但是|a26|<a1 , |a27|<a2 , …,|a49|<a24
∴S1 , S2 , …,S25中都为正,而S26 , S27 , …,S50都为正
同理S1 , S2 , …,s75都为正,S1 , S2 , …,s75 , …,s100都为正,
故选D
由于f(n)=sin ![]() 的周期T=50,由正弦函数性质可知,a1 , a2 , …,a24>0,a26 , a27 , …,a49<0,f(n)=
的周期T=50,由正弦函数性质可知,a1 , a2 , …,a24>0,a26 , a27 , …,a49<0,f(n)= ![]() 单调递减,a25=0 , a26…a50都为负数,但是|a26|<a1 , |a27|<a2 , …,|a49|<a24 , 从而可判断
单调递减,a25=0 , a26…a50都为负数,但是|a26|<a1 , |a27|<a2 , …,|a49|<a24 , 从而可判断


科目:高中数学 来源: 题型:
【题目】某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了![]() 件产品作为样本,检测一项质量指标值,若该项质量指标值落在
件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表
内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表![]() 是设备改造后的样本的频数分布表.
是设备改造后的样本的频数分布表.
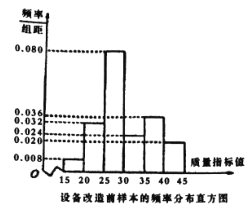
表:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据频率分布直方图和表 提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在![]() 内的定为一等品,每件售价
内的定为一等品,每件售价![]() 元;质量指标值落在
元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价
内的定为二等品,每件售价![]() 元;其它的合格品定为三等品,每件售价
元;其它的合格品定为三等品,每件售价![]() 元.根据表
元.根据表![]() 的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lg(x+1)
(1)若0<f(1﹣2x)﹣f(x)<1,求x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,g(x)=f(x),求函数y=g(x)(x∈[1,2])的反函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为6的正方形![]() 中,弧
中,弧![]() 的圆心为
的圆心为![]() ,过弧
,过弧![]() 上的点
上的点![]() 作弧
作弧![]() 的切线,与
的切线,与![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 边于点
边于点![]() .
.
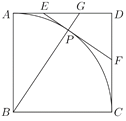
(1)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出函数定义域;
之间的函数解析式,并写出函数定义域;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
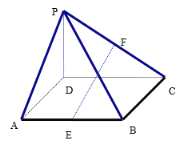
(1)求证:AB⊥平面PAD;
(2)求证:EF//平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的对边分别为A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com