
【题目】已知点P(1,2)在抛物线C:y2=2px(p>0)上.
(Ⅰ)求C的方程;
(Ⅱ)斜率为﹣1的直线与C交于异于点P的两个不同的点M,N,若直线PM,PN分别与x轴交于A,B两点,求证:△PAB为等腰三角形.
【答案】(Ⅰ) y2=4x; (Ⅱ)见解析
【解析】
(Ⅰ) 将点P(1,2)代入抛物线方程可得结果;
(Ⅱ) 设直线MN的方程为y=﹣x+t,联立抛物线方程y2=4x,根据韦达定理和斜率公式运算可得.
(Ⅰ)将点P(1,2)代入抛物线方程可得22=2p1,∴p=2,所以抛物线方程为y2=4x;
(Ⅱ)证明:由题意设直线MN的方程为y=﹣x+t,联立抛物线方程y2=4x,可得x2﹣(2t+4)x+t2=0,
设M(x1,y1),N(x2,y2),可得x1+x2=2t+4,x1x2=t2,
由kPM+kPN![]() 2+(t﹣3)(
2+(t﹣3)(![]() )
)
=﹣2+(t﹣3)![]() 2+2(t﹣3)
2+2(t﹣3)![]() 0,
0,
则∠PAB=∠PBA,即△PAB为等腰三角形.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】某学校为了解本校文、理科学生的学业水平模拟测试数学成绩情况,分别从理科班学生中随机抽取![]() 人的成绩得到样本甲,从文科班学生中随机抽取
人的成绩得到样本甲,从文科班学生中随机抽取![]() 人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:
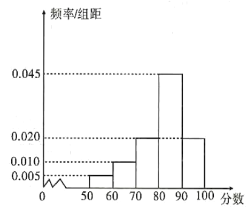
甲样本数据直方图
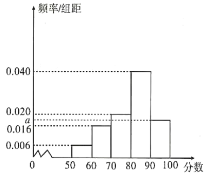
乙样本数据直方图
已知乙样本中数据在![]() 的有
的有![]() 个.
个.
(1)求![]() 和乙样本直方图中
和乙样本直方图中![]() 的值;
的值;
(2)试估计该校理科班学生本次模拟测试数学成绩的平均值和文科班学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解观众对某综艺节目的评价情况,栏目组随机抽取了![]() 名观众进行评分调查(满分
名观众进行评分调查(满分![]() 分),并统计得到如图所示的频率分布直方图,以下说法错误的是( )
分),并统计得到如图所示的频率分布直方图,以下说法错误的是( )
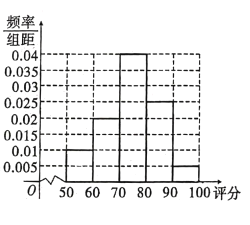
A.参与评分的观众评分在![]() 的有
的有![]() 人
人
B.观众评分的众数约为![]() 分
分
C.观众评分的平均分约为![]() 分
分
D.观众评分的中位数约为![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,记
,记![]()
(1)求实数![]() 、
、![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)对于任意满足![]()
![]() 的自变量
的自变量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如果存在一个常数
,如果存在一个常数![]() ,使得定义在区间
,使得定义在区间![]() 上的一个函数
上的一个函数![]() ,有
,有![]()
![]() 恒成立,则称
恒成立,则称![]() 为区间
为区间![]() 上的有界变差函数,试判断
上的有界变差函数,试判断![]() 是否区间
是否区间![]() 上的有界变差函数,若是,求出
上的有界变差函数,若是,求出![]() 的最小值;若不是,请说明理由.
的最小值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() .若数列
.若数列![]() 满足
满足![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“伴随数列”.
的“伴随数列”.
(1)数列1,3,5,7,9是否存在“伴随数列”,若存在,写出其“伴随数列”;若不存在,请说明理由;
(2)若![]() 为
为![]() 的“伴随数列”,证明:
的“伴随数列”,证明:![]() ;
;
(3)已知数列![]() 存在“伴随数列”
存在“伴随数列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆E的长轴和短轴为对角线的四边形的面积为
,以椭圆E的长轴和短轴为对角线的四边形的面积为![]() .
.
(1)求椭圆E的方程;
(2)若直线![]() 与椭圆E相交于A,B两点,设P为椭圆E上一动点,且满足
与椭圆E相交于A,B两点,设P为椭圆E上一动点,且满足![]() (O为坐标原点).当
(O为坐标原点).当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,过
中,过![]() 轴正方向上一点
轴正方向上一点![]() 任作一直线,与抛物线
任作一直线,与抛物线![]() 相交于
相交于![]() 两点,一条垂直于
两点,一条垂直于![]() 轴的直线分别与线段
轴的直线分别与线段![]() 和直线
和直线![]() 交于点
交于点![]() .
.
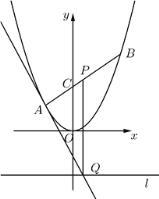
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 与该抛物线有且仅有一个公共点.
与该抛物线有且仅有一个公共点.
(3)若直线![]() 的斜率存在,且与该抛物线有且仅有一个公共点,试问
的斜率存在,且与该抛物线有且仅有一个公共点,试问![]() 是否一定为线段
是否一定为线段![]() 的中点?说明理由.
的中点?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+1|(a∈R),g(x)=|2x﹣1|+2.
(1)若a=1,证明:不等式f(x)≤g(x)对任意的x∈R成立;
(2)若对任意的m∈R,都有t∈R,使得f(m)=g(t)成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com