
 的模是向量
的模是向量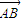 的模的t倍,
的模的t倍,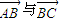 的夹角为θ,那么我们称向量
的夹角为θ,那么我们称向量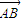 经过一次(t,θ)变换得到向量
经过一次(t,θ)变换得到向量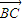 .在直角坐标平面内,设起始向量
.在直角坐标平面内,设起始向量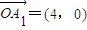 ,向量
,向量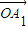 经过n-1次
经过n-1次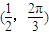 变换得到的向量为
变换得到的向量为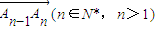 ,其中
,其中 为逆时针排列,记Ai坐标为(ai,bi)(i∈N*),则下列命题中不正确的是( )
为逆时针排列,记Ai坐标为(ai,bi)(i∈N*),则下列命题中不正确的是( )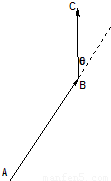
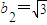
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
 (2012•九江一模)已知点G是△ABC的外心,
(2012•九江一模)已知点G是△ABC的外心,| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| GA |
| AB |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•松江区二模)如图所示,向量
(2013•松江区二模)如图所示,向量| BC |
| AB |
| AB |
| BC |
| AB |
| BC |
| OA1 |
| OA1 |
| 1 |
| 2 |
| 2π |
| 3 |
| An-1An |
查看答案和解析>>
科目:高中数学 来源: 题型:
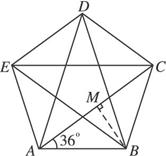
A.5 B.10 C.15 D.20
查看答案和解析>>
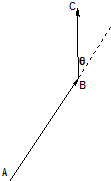
科目:高中数学 来源:松江区二模 题型:单选题
| BC |
| AB |
| AB |
| BC |
| AB |
| BC |
| OA1 |
| OA1 |
| 1 |
| 2 |
| 2π |
| 3 |
| An-1An |
A.b2=
| ||
| B.b3k+1-b3k=0(k∈N*) | ||
| C.a3k+1-a3k-1=0(k∈N*) | ||
| D.8(ak+4-ak+3)+(ak+1-ak)=0(k∈N*) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com