Question

20．已知函数f（x）=$\frac{ax}{{e}^{x-1}}$（a∈R），g（x）=$\frac{b}{{e}^{x}}$+$\frac{{e}^{-1}}{2x+{e}^{x}}$（b∈R），其中e为自然对数的底数．（参考数据：e²≈7.39，e${\;}^{\frac{1}{4}}$≈1.28，e${\;}^{\frac{1}{2}}$≈1.65）
（1）讨论函数f（x）的单调性；
（2）若a=1时，函数y=f（2x）+g（x）有三个零点，分别记为x₁、x₂、x₃（x₁＜x₂＜x₃），证明：-2＜4（x₁+x₂）＜3．

Answer 1

分析 （1）求出函数的导数，通过讨论a的范围，求出函数的单调区间即可；
（2）令$t=\frac{2x}{{{e^{x-1}}}}+e$，得到t²+（b-e）t+1=0，设方程t²+（b-e）t+1=0的根为t₁、t₂，结合函数图象证明即可．

解答 解：（1）因为$f（x）=\frac{ax}{{{e^{x-1}}}}=ae（{\frac{x}{e^x}}）$的定义域为实数R，
所以$f'（x）=ae（{\frac{1-x}{e^x}}）$．
①当a=0时，f（x）=0是常数函数，没有单调性．
②当a＜0时，由f'（x）＜0，得x＜1；由f'（x）＞0，得x＞1．
所以函数f（x）在（-∞，1）上单调递减，在（1，+∞）上单调递增．
③当a＞0时，由f'（x）＜0得，x＞1； 由f'（x）＞0，得x＜1，
所以函数f（x）在（1，+∞）上单调递减，在（-∞，1）上单调递增．
（2）因为a=1，f（2x）+g（x）=0，
所以$\frac{2x}{{{e^{2x-1}}}}+\frac{b}{e^x}+\frac{{{e^{-1}}}}{{2x+{e^x}}}=0$，即$\frac{2x}{{{e^{x-1}}}}+b+\frac{{{e^{x-1}}}}{{2x+{e^x}}}=\frac{2x}{{{e^{x-1}}}}+b+\frac{1}{{\frac{{2x+{e^x}}}{{{e^{x-1}}}}}}=0$．
令$t=\frac{2x}{{{e^{x-1}}}}+e$，则有$t-e+b+\frac{1}{t}=0$，即t²+（b-e）t+1=0．
设方程t²+（b-e）t+1=0的根为t₁、t₂，则t₁•t₂=1，
所以x₁、x₂、x₃是方程${t_1}=\frac{2x}{{{e^{x-1}}}}+e…（*），{t_2}=\frac{2x}{{{e^{x-1}}}}+e…（{**}）$的根．
由（1）知$t=\frac{2x}{{{e^{x-1}}}}+e$在（-∞，1）单调递增，在（1，+∞）上单调递减．
且当x→-∞时，t→-∞，当x→+∞时，t→e，t_max=t（1）=2+e，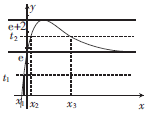

如图，依据题意，不妨取e＜t₂＜e+2，所以$\frac{1}{e+2}＜{t_1}=\frac{1}{t_2}＜\frac{1}{e}$，
因为$t（{-\frac{1}{2}}）=-{e^{\frac{3}{2}}}+e=e（{-{e^{\frac{1}{2}}}+1}）＜0，t（{-\frac{1}{4}}）=e（{-\frac{1}{2}{e^{\frac{5}{4}}}+e}）={e^2}（{-\frac{1}{2}{e^{\frac{1}{4}}}+1}）＞1$，
易知0＜x₂＜1，要证-2＜4（x₁+x₂）＜3，即证$-\frac{1}{2}＜{x_1}＜-\frac{1}{4}$．
所以$t（{-\frac{1}{2}}）＜0＜t（{x_1}）＜\frac{1}{e}＜t（{-\frac{1}{4}}）$，又函数y=t（x）在（-∞，1）上单调递增，
所以$-\frac{1}{2}＜{x_1}＜-\frac{1}{4}$，所以-2＜4（x₁+x₂）＜3．

点评 本题考查了函数的单调性、最值问题，考查导数的应用以及分类讨论思想，转化思想，数形结合思想，是一道综合题．