
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 有且只有一个公共点,求正数
有且只有一个公共点,求正数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减;当
递减;当![]() 时,
时, ![]() 在
在![]() 递增;当
递增;当![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增.(2)
递增.(2)![]() 或
或![]() .
.
【解析】
(1)根据函数解析式,求得导函数,并对![]() 分类讨论,即可判断函数
分类讨论,即可判断函数![]() 的单调性;
的单调性;
(2)根据切点横坐标,代入方程求得切点坐标,结合导数的几何意义即可求得切线方程;联立直线方程与函数解析式,由切线![]() 与
与![]() 有且只有一个公共点可知联立后的方程有且仅有一个根,构造函数
有且只有一个公共点可知联立后的方程有且仅有一个根,构造函数![]() ,并求得导函数,对
,并求得导函数,对![]() 分类讨论,即可判断函数的单调性和最值,进而求得正数
分类讨论,即可判断函数的单调性和最值,进而求得正数![]() 的取值范围.
的取值范围.
(1)函数![]() ,定义域为
,定义域为![]() ,
,
![]()
当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 在
在![]() 递减,
递减,
![]() 时,
时,![]() ,
,![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 在
在![]() 递增,
递增,
![]() 时,
时,![]() ,
,![]() 在
在![]() 递减;
递减;
综上所述,当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减;
递减;
当![]() 时,
时, ![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增.
递增.
(2)当![]() 时,代入函数解析式可得
时,代入函数解析式可得![]() ,则切点坐标为
,则切点坐标为![]() ;
;
代入导函数可得切线的斜率为![]() ,
,
由点斜式可得切线方程为![]() ,化简可得
,化简可得![]() ,
,
则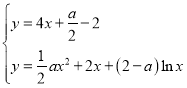 整理可得
整理可得![]() ,
,
令![]() ,
,
由题意可知函数![]() 有且只有一个零点,
有且只有一个零点, ,
,
1 当![]() 时,由
时,由![]() ,解得
,解得![]() .
.
且当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() 是
是![]() 唯一的极小值点,也是最小值点.
唯一的极小值点,也是最小值点.
且![]() ,故
,故![]() 满足题意.
满足题意.
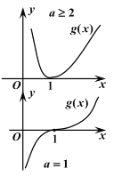
2 当![]() 时.由
时.由![]() 解得
解得![]() ,
,![]() .
.
(1)当![]() 时,
时,![]() ,
,![]() 单调递增,又
单调递增,又![]() ,
,
所以![]() 满足题意.
满足题意.
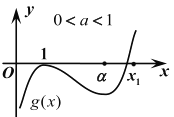
(2)当![]() 时,当
时,当![]() ,
,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() .
.
又存在![]() ,所以
,所以![]() ,
,
![]() .
.
在![]() 内,
内,![]() 存在零点,所以
存在零点,所以![]() 至少有两个零点,不合题意.
至少有两个零点,不合题意.
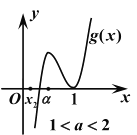
当![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() .
.
又存在![]() ,并注意到
,并注意到![]() ,
,![]() ,
,
![]() ,所以在
,所以在![]() 内
内![]() 存在零点,
存在零点,
从而![]() 至少有两个零点,不合题意.
至少有两个零点,不合题意.
综上所述,![]() 或
或![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,若
,每单提成4元,若![]() ,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若
,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
表1:美团外卖配送员甲送餐量统计
日送餐量x(单) | 13 | 14 | 16 | 17 | 18 | 20 |
天数 | 2 | 6 | 12 | 6 | 2 | 2 |
表2:饿了么外卖配送员乙送餐量统计
日送餐量x(单) | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)设美团外卖配送员月工资为![]() ,饿了么外卖配送员月工资为
,饿了么外卖配送员月工资为![]() ,当
,当![]() 时,比较
时,比较![]() 与
与![]() 的大小关系
的大小关系
(2)将4月份的日送餐量的频率视为日送餐量的概率
(ⅰ)计算外卖配送员甲和乙每日送餐量的数学期望E(X)和E(Y)
(ⅱ)请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 过点
过点![]() ,过抛物线E上一点
,过抛物线E上一点![]() 作两直线PM,PN与圆C:
作两直线PM,PN与圆C:![]() 相切,且分别交抛物线E于M、N两点.
相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
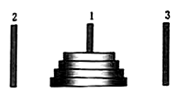
【题目】如图所示,有三根针和套在一根针上的![]() 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.
将![]() 个金属片从1号针移到3号针最少需要移动的次数记为
个金属片从1号针移到3号针最少需要移动的次数记为![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知曲线
轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),射线
),射线![]() ,
,![]() ,
,![]() 分别与曲线
分别与曲线![]() 交于极点
交于极点![]() 外的三点
外的三点![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 两点在曲线
两点在曲线![]() 上,求
上,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为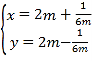 (m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
(m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+![]() )=1.
)=1.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)已知点M (2,0),若直线l与曲线C相交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年篮球世界杯在中国举行,中国男篮由于主场作战而备受观众瞩目.为了调查国人对中国男篮能否进入十六强持有的态度,调查人员随机抽取了男性观众与女性观众各100名进行调查,所得情况如下表所示:
男性观众 | 女性观众 | |
认为中国男篮能够进入十六强 | 60 | |
认为中国男篮不能进入十六强 |
若在被抽查的200名观众中随机抽取1人,抽到认为中国男篮不能进入十六强的女性观众的概率为![]() .
.
(1)完善上述表格;
(2)是否有99%的把握认为性别与对中国男篮能否进入十六强持有的态度有关?
附: ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com