设AB是单位圆O的直径,N是圆上的动点,过点N的切线与过点A、B的切线分别交于D、C两点.四边形ABCD的对角线AC和BD的交点为G,求G的轨迹.
解:以圆心O为原点,直径AB为x轴建立直角坐标系,
则A(-1,0),B(1,0),单位圆的方程为x
2+y
2=1,
设N的坐标为(cosθ,sinθ),则切线DC的方程为:xcosθ+ysinθ=1,
由此可得C(1,

),D(-1,

),
AC的方程为y=

(x+1),
BD的方程为y=-

(x-1),
将两式相乘得:y
2=
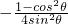
(x
2-1),
即x
2+4y
2=1
当点N恰为A或B时,四边形ABCD变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以G的轨迹方程为x
2+4y
2=1,(-1<x<1).
分析:要求G的轨迹,需建立直角坐标系,故以圆心O为原点,直径AB为x轴建立直角坐标系,则A(-1,0),B(1,0),单位圆的方程为x
2+y
2=1,再设出N(cosθ,sinθ),从而得到DC的方程,从而有C、D的坐标与直线AC、BD的方程,继而可求得G的轨迹.
点评:本题考查直线和圆的方程的应用,关键在于建立适当的直角坐标系,求得直线DC、AC、BD的方程,消掉参数即可,易错点在于G的轨迹方程为x
2+4y
2=1,(-1<x<1),不是整个椭圆,属于难题.

 ),D(-1,
),D(-1, ),
), (x+1),
(x+1), (x-1),
(x-1),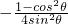 (x2-1),
(x2-1),

 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.