
已知![]() ,
,![]() ,
,![]() 成等差数列,且公差为
成等差数列,且公差为![]() ,
,![]() 为实常数,则
为实常数,则![]() ,
,![]() ,
,![]() 这三个三角函数式的算术平均数为____________________。
这三个三角函数式的算术平均数为____________________。
![]()
[试题解析]
考查知识点:本题考察了等差数列、算术平均数的概念及三角函数式的恒等变形。
解题思路:先利用倍角公式的变形把次数由二次降为一次,再利用和角公式、差角公式来统一角,达到化简求值的目的。
解题过程:
由题意,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
∴![]() ,
,![]() ,
,![]() 这三个三角函数式的算术平均数为
这三个三角函数式的算术平均数为
![]()
![]()
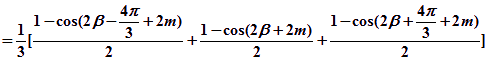
![]()
![]()
![]()
![]() 。
。
解题方法技巧:本题的关键是三角函数式的化简,在化简时要及时调控变形方向,把握好 “角的变化”、 “函数名称的变化”、“运算形式的变化”这三种三角变换的时机。
[试题评析]
命题意图:考察学生综合利用所学知识的能力、推理变形能力。
试题点评:本题的综合性较高,对学生利用三角公式进行三角恒等变换的能力要求较高。
对考点的发散思维点拨:新课标中的三角函数的考察要想推陈出新,可以不断改变考察方式和考察角度。
引导、归纳及预测:虽然大纲中对三角函数的要求近年来有所降低,但对知识点的综合性却在提高,三角函数部分与其它章节的综合也在意料之中。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com