
【题目】为了比较注射![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .
.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)下表1和表2分别是注射药物![]() 和
和![]() 后的试验结果.(疱疹面积单位:
后的试验结果.(疱疹面积单位: ![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
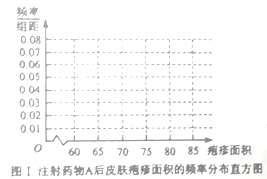
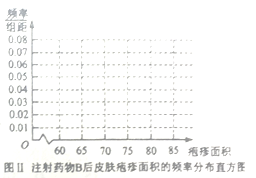
(ⅱ)完成下面![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“注射药物
的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
表3:

附: 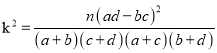
【答案】(1) ![]() ;(2)(i)答案见解析;(2)答案见解析.
;(2)(i)答案见解析;(2)答案见解析.
【解析】试题分析:(1)利用组合数找出所有事件的个数n,基本事件的个数m,代入古典概率计算公式p=![]() ;(2)(ⅰ)由频数分布表中的频数求出每组的
;(2)(ⅰ)由频数分布表中的频数求出每组的![]() ,画出频率分布直方图,可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数,(ⅱ)完成2×2列联表,代入
,画出频率分布直方图,可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数,(ⅱ)完成2×2列联表,代入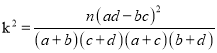 计算随机变量值后与临界点比较,判断能否有
计算随机变量值后与临界点比较,判断能否有![]() 的把握认为“注射药物
的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
试题解析:
(Ⅰ)甲、乙两只家兔分在不同组的概率为
![]()
(Ⅱ)(i)
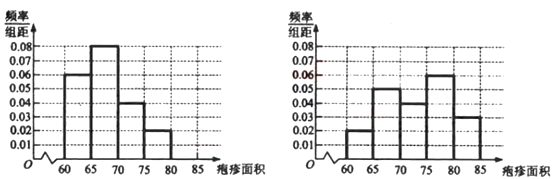
图Ⅰ注射药物A后皮肤疱疹面积的频率分布直方图 图Ⅱ注射药物B后皮肤疱疹面积的频率分布直方图
可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.
(ii)表3:
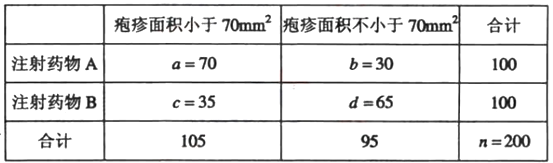
![]()
由于K2>10.828,所以有99.9%的把握认为“注射药物A后的疱疹面积于注射药物B后的疱疹面积有差异”。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知直线l:![]()
![]() 1
1![]() 证明直线l经过定点并求此点的坐标;
证明直线l经过定点并求此点的坐标;
![]() 2
2![]() 若直线l不经过第四象限,求k的取值范围;
若直线l不经过第四象限,求k的取值范围;
![]() 3
3![]() 若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设![]() 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCFE中,四边形EFCB为梯形,EF∥BC,且EF= ![]() BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG=
BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG= ![]() ,CF=
,CF= ![]() ,BF=
,BF= ![]() .
. 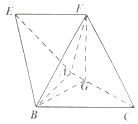
(1)证明:平面FGB⊥平面ABC;
(2)求二面角E﹣AB﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点 ![]() ,点P是圆
,点P是圆 ![]() 上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
(1)求点E的轨迹方程;
(2)已知M,N两点的坐标分别为(﹣2,0),(2,0),点T是直线x=4上的一个动点,且直线TM,TN分别交(1)中点E的轨迹于C,D两点(M,N,C,D四点互不相同),证明:直线CD恒过一定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
,![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
,![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣alnx﹣(a﹣2)x.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2(1)求满足条件的最小正整数a的值;
(Ⅲ)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com