
【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
科目:高中数学 来源: 题型:
【题目】为了比较注射![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .
.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)下表1和表2分别是注射药物![]() 和
和![]() 后的试验结果.(疱疹面积单位:
后的试验结果.(疱疹面积单位: ![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(ⅱ)完成下面![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“注射药物
的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
表3:

附: 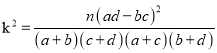
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)经过点(﹣1,
=1(a>b>0)经过点(﹣1, ![]() ),其离心率e=
),其离心率e= ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l:y=kx+m与椭圆C相切,切点为T,且l与直线x=﹣4相交于点S.
试问:在x轴上是否存在一定点,使得以ST为直径的圆恒过该定点?若存在,求出该点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足 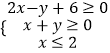 ,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
A.[﹣1,2]
B.[﹣2,1]
C.[2,3]
D.[﹣1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在线段PD上.
,PA=2,点M在线段PD上. 
(1)求证:AB⊥PC.
(2)若二面角M﹣AC﹣D的大小为45°,求BM与平面PAC所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个.从袋子中不放回地随机抽取小球两个,每次抽取一个球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1)记事件![]() 表示“
表示“![]() ”,求事件
”,求事件![]() 的概率;
的概率;
(2)在区间![]() 内任取两个实数
内任取两个实数![]() ,
,![]() ,求“事件
,求“事件![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com