
|
| αn-1 |
| n |
| αn-1 |
| n |
| a1 |
| 2 |
| ak |
| k+1 |
| (k+1)(k+2) |
| k+1 |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
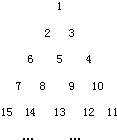 把正整数数列{n}中的数按如下规律排成三角形数阵:设 ai,j是位于这个三角形数表中从上往下数第i行,从左往 右数第j个数(如a1,1=1,a4,3=9).若am,n=2010,求m+n=
把正整数数列{n}中的数按如下规律排成三角形数阵:设 ai,j是位于这个三角形数表中从上往下数第i行,从左往 右数第j个数(如a1,1=1,a4,3=9).若am,n=2010,求m+n=查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x2 |
| 1 |
| an+12 |
| ||
(3n-1)
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| Bn | n |
查看答案和解析>>
科目:高中数学 来源:东北育才学校2008-2009学年度高三模拟试题(理科数学) 2009.5.20 题型:013
数列{αn}中,α1=2,![]() ,
,![]() ,又
,又![]() ,则S2008=
,则S2008=
A.111.5
B.112.5
C.113.5
D.114.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com