
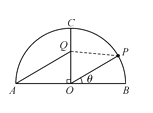
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)设∠OPQ=α,在△POQ中,用正弦定理![]() 可得含α,θ的关系式,将其展开化简并整理后得tanα=
可得含α,θ的关系式,将其展开化简并整理后得tanα=![]() ,将θ=
,将θ=![]() 代入得答案;
代入得答案;
(2)令f(θ)=![]() 并利用导数求得f(θ)的最大值,即此时的
并利用导数求得f(θ)的最大值,即此时的![]() ,由(1)可知tanα=
,由(1)可知tanα=![]() ,得答案.
,得答案.
(1)设∠OPQ=α,在△POQ中,用正弦定理可得含α,θ的关系式.
因为∠AQC=![]() ,所以∠AQO=
,所以∠AQO=![]() .又OA=OB=3,所以OQ=
.又OA=OB=3,所以OQ=![]()
在△OPQ中,OQ=![]() ,OP=3,∠POQ=
,OP=3,∠POQ=![]() -θ,设∠OPQ=α,则∠PQO=
-θ,设∠OPQ=α,则∠PQO=![]() -α+θ.
-α+θ.
由正弦定理,得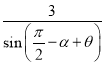 =
=![]() ,即
,即![]() sinα=cos(α-θ).
sinα=cos(α-θ).
展开并整理,得tanα=![]() ,其中θ∈
,其中θ∈![]() .
.
此时当θ=![]() 时,tanα=
时,tanα=![]() .因为α∈(0,π),所以α=
.因为α∈(0,π),所以α=![]() .
.
故当θ=![]() 时,∠OPQ=
时,∠OPQ=![]() .
.
(2)设f(θ)=![]() ,θ∈
,θ∈![]() .
.
则f′(θ)=![]() =
=![]() .
.
令f′(θ)=0,得sinθ=![]() ,记锐角θ0满足
,记锐角θ0满足![]() ,
,
则![]() ,即
,即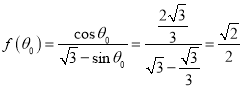
列表如下:
θ | (0,θ0) | θ0 |
|
f′(θ) | + | 0 | - |
f(θ) | 单调递增 |
| 单调递减 |
由上表可知,f(θ0)=![]() 是极大值,也是最大值.
是极大值,也是最大值.
由(1)可知tanα=f(θ)>0,则![]() , tanα单调递增
, tanα单调递增
则当tanα取最大值![]() 时,α也取得最大值.
时,α也取得最大值.
故游客在观赏亭P处的观赏效果最佳时,sinθ=![]() .
.


科目:高中数学 来源: 题型:
【题目】某学生参加4门学科的学业水平测试,每门得![]() 等级的概率都是
等级的概率都是![]() ,该学生各学科等级成绩彼此独立.规定:有一门学科获
,该学生各学科等级成绩彼此独立.规定:有一门学科获![]() 等级加1分,有两门学科获
等级加1分,有两门学科获![]() 等级加2分,有三门学科获
等级加2分,有三门学科获![]() 等级加3分,四门学科全获
等级加3分,四门学科全获![]() 等级则加5分,记
等级则加5分,记![]() 表示该生的加分数,
表示该生的加分数, ![]() 表示该生获
表示该生获![]() 等级的学科门数与未获
等级的学科门数与未获![]() 等级学科门数的差的绝对值.
等级学科门数的差的绝对值.
(1)求![]() 的数学期望;
的数学期望;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人上午的工作时间和加工的零件数,点
名工人上午的工作时间和加工的零件数,点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人下午的工作时间和加工的零件数,
名工人下午的工作时间和加工的零件数,![]() .记
.记![]() 为第
为第![]() 名工人在这一天中加工的零件总数,记
名工人在这一天中加工的零件总数,记![]() 为第
为第![]() 名工人在这一天中平均加工的零件数,则
名工人在这一天中平均加工的零件数,则![]() ,
,![]() ,
,![]() 中的最大值与
中的最大值与![]() ,
,![]() ,
,![]() 中的最大值分别是( )
中的最大值分别是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某无缝钢管厂只生产甲、乙两种不同规格的钢管,钢管有内外两个口径,甲种钢管内外两口径的标准长度分别为![]() 和
和![]() ,乙种钢管内外两个口径的标准长度分别为
,乙种钢管内外两个口径的标准长度分别为![]() 和
和![]() .根据长期的生产结果表明,两种规格钢管每根的长度
.根据长期的生产结果表明,两种规格钢管每根的长度![]() 都服从正态分布
都服从正态分布![]() ,长度在
,长度在![]() 之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
(1)在该钢管厂生产的钢管中随机抽取10根进行检测,求至少有1根为废品的概率;
(2)监管部门规定每种规格钢管的“口径误差”的计算方式为:若钢管的内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() ,则“口径误差”为
,则“口径误差”为![]() ,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是![]() (正品钢管中没有“口径误差”大于
(正品钢管中没有“口径误差”大于![]() 的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
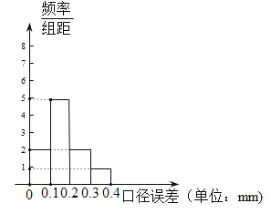

甲种钢管 乙种钢管
已知经销商经销甲种钢管,其中“一级品”的利润率为0.3,“二级品”的利润率为0.18,“合格品”的利润率为0.1;经销乙种钢管,其中“一级品”的利润率为0.25,“二级品”的利润率为0.15,“合格品”的利润率为0.08,若视频率为概率.
(ⅰ)若经销商对甲、乙两种钢管各进了100万元的货,![]() 和
和![]() 分别表示经销甲、乙两种钢管所获得的利润,求
分别表示经销甲、乙两种钢管所获得的利润,求![]() 和
和![]() 的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
(ⅱ)若经销商计划对甲、乙两种钢管总共进100万元的货,则分别在甲、乙两种钢管上进货多少万元时,可使得所获利润的方差和最小?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园要设计如图所示的景观窗格(其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,如图二中所示多边形![]() ),整体设计方案要求:内部井字形的两根水平横轴
),整体设计方案要求:内部井字形的两根水平横轴![]() 米,两根竖轴
米,两根竖轴![]() 米,记景观窗格的外框(如图二实线部分,轴和边框的粗细忽略不计)总长度为
米,记景观窗格的外框(如图二实线部分,轴和边框的粗细忽略不计)总长度为![]() 米.
米.

(1)若![]() ,且两根横轴之间的距离为
,且两根横轴之间的距离为![]() 米,求景观窗格的外框总长度;
米,求景观窗格的外框总长度;
(2)由于预算经费限制,景观窗格的外框总长度不超过![]() 米,当景观窗格的面积(多边形
米,当景观窗格的面积(多边形![]() 的面积)最大时,给出此景观窗格的设计方案中
的面积)最大时,给出此景观窗格的设计方案中![]() 的大小与
的大小与![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
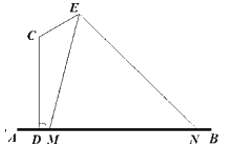
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
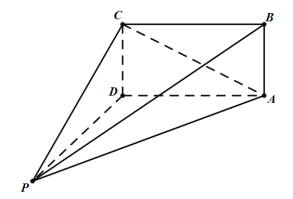
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共1000名男生中随机抽取50人测量身高,据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
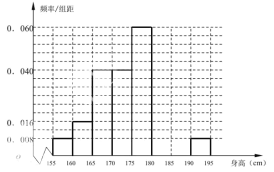
(1)求第六组、第七组的频率,并估计高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)学校决定让这五十人在运动会上组成一个高旗队,在这五十人中要选身高在![]() 以上(含
以上(含![]() )的两人作为队长,求这两人在同一组的概率.
)的两人作为队长,求这两人在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com