
分析 (1)曲线C的极坐标方程化为${ρ}^{2}=2\sqrt{3}ρsinθ$,由此能求出曲线C的直角坐标方.
(2)P的坐标为$(\sqrt{3},0)$,将l的参数方程代入曲线C的直角坐标方程得:${t^2}-(3+\sqrt{3})t+3=0$,由此能求出|PD|的长.
解答 解:(1)∵曲线C的极坐标方程为$ρ=2\sqrt{3}sinθ$,
∴${ρ}^{2}=2\sqrt{3}ρsinθ$,
∴x2+y2=2$\sqrt{3}y$,
∴曲线C的直角坐标方程为${x^2}+{(y-\sqrt{3})^2}=3$.
(2)P的坐标为$(\sqrt{3},0)$,在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}-\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$(t为参数),
将l的参数方程代入曲线C的直角坐标方程得:${t^2}-(3+\sqrt{3})t+3=0$,
设点A,B,D对应的参数分别为t1,t2,t3,
则${t_1}+{t_2}=3+\sqrt{3}$,t1t2=3,
$|PD|=|{t_3}|=|\frac{{{t_1}+{t_2}}}{2}|=\frac{{3+\sqrt{3}}}{2}$,
∴|PD|的长为$\frac{{3+\sqrt{3}}}{2}$.
点评 本题考查参数方程与极坐标方程的互化,考查线段长的求法,是中档题,解题时要认真审题,注意直角坐标方程与极坐标方程互化公式的合理运用.


科目:高中数学 来源: 题型:解答题
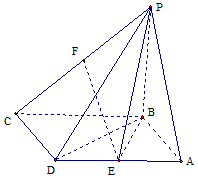 如图,四棱锥P-ABCD的底面是平行四边形,BA=BD=$\sqrt{2}$,AD=2,PA=PD=$\sqrt{5}$,E,F分别是棱AD,PC的中点.
如图,四棱锥P-ABCD的底面是平行四边形,BA=BD=$\sqrt{2}$,AD=2,PA=PD=$\sqrt{5}$,E,F分别是棱AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=-2x | B. | y2=-4x | C. | y2=2x | D. | y2=-4x或y2=4x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列三个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列三个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b=1 | B. | a+b=3m | C. | ab=1 | D. | b=am |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
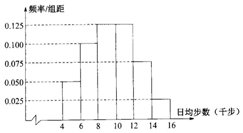 某单位委托一家网络调查公司对单位1000名职员进行了QQ运动数据调查,绘制了日均行走步数(千步)的频率分布直方图,如图所示(每个分组包括左端点,不包括右端点,如第一组表示运动量在[4,6)之间(单位:千步)).
某单位委托一家网络调查公司对单位1000名职员进行了QQ运动数据调查,绘制了日均行走步数(千步)的频率分布直方图,如图所示(每个分组包括左端点,不包括右端点,如第一组表示运动量在[4,6)之间(单位:千步)).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com