
(本小题满分12分)
小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
(1) ;(2)分布列详见解析,
;(2)分布列详见解析,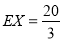 .
.
【解析】
试题分析:本题主要考查二项分布、离散型随机变量的分布列和数学期望等基础知识,意在考查考生的分析问题解决问题的能力、运算求解能力.第一问,发放一次红包,每个人得到的概率为 ,两次中,其中一次得到,一次没得到,所以
,两次中,其中一次得到,一次没得到,所以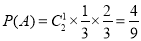 ;第二问,先写出X的所有可能值,当
;第二问,先写出X的所有可能值,当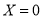 时,说明5元的2个和10元的1个都没有得到,当
时,说明5元的2个和10元的1个都没有得到,当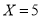 时,说明5元的2个红包得到了1个,10元的没有得到,当
时,说明5元的2个红包得到了1个,10元的没有得到,当 时,说明5元的2个得到了,10元的没有得到,或者5元的2个都没有得到,10元的得到了,当
时,说明5元的2个得到了,10元的没有得到,或者5元的2个都没有得到,10元的得到了,当 时,5元的2个红包得到了1个,10元的得到了,当
时,5元的2个红包得到了1个,10元的得到了,当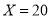 时,说明5元的2个都得到了,10元的1个也得到了,分别利用二项分布和独立事件求出概率,最后利用
时,说明5元的2个都得到了,10元的1个也得到了,分别利用二项分布和独立事件求出概率,最后利用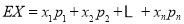 求出数学期望.
求出数学期望.
试题解析:(Ⅰ)设“甲恰得一个红包”为事件A,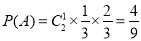 . 4分
. 4分
(Ⅱ)X的所有可能值为0,5,10,15,20.
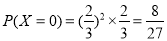 ,
,
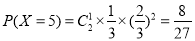 ,
,
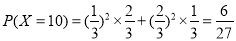 ,
,
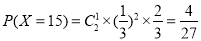 ,
,
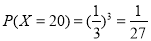 . 10分
. 10分
X的分布列:
X | 0 | 5 | 10 | 15 | 20 |
P |
|
|
|
|
|
E(X)=0×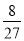 +5×
+5×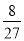 +10×
+10×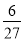 +15×
+15×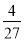 +20×
+20×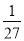 =
= . 12分
. 12分
考点:二项分布、离散型随机变量的分布列和数学期望.
考点分析: 考点1:古典概率 试题属性

科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: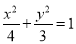 ,直线
,直线 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线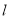 的普通方程;
的普通方程;
(Ⅱ)设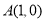 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线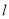 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
设x,y满足约束条件 ,则
,则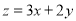 的最大值为( )
的最大值为( )
A.8 B.9 C.28 D.29
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: ,直线
,直线 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线 的普通方程;
的普通方程;
(Ⅱ)设 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试一文科数学试卷(解析版) 题型:选择题
已知圆 的圆心为坐标原点,半径为
的圆心为坐标原点,半径为 ,直线
,直线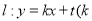 为常数,
为常数,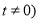 与圆
与圆 相交于
相交于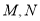 两点,记△
两点,记△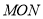 的面积为
的面积为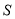 ,则函数
,则函数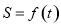 的奇偶性为( )
的奇偶性为( )
A.偶函数 B.奇函数
C.既不是偶函数,也不是奇函数 D.奇偶性与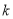 的取值有关
的取值有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com