设函数f(x)=2x2+bln(x+1),其中b≠0.
(1)当b=-1时,求在曲线y=f(x)上一点(0,f(0)处的切线方程;
(2)求函数f(x)的极值点.
解:(1)当b=-1时,f(x)=2x
2-ln(x+1),f(0)=0,
f′(x)=4x-

,
在点(0,f(0))处的切线斜率k=f′(0)=-1,
所以所求切线方程为:y=-x;
(2)函数f(x)=2x
2+bln(x+1)的定义域为(-1,+∞),
f′(x)=4x+
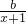
=
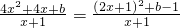
,
①当b≥1时,f′(x)≥0,函数f(x)在(-1,+∞)上单调递增,无极值点;
②当b<1时,解f′(x)=0得两个不同解
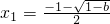
,
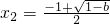
,
当b<0时,
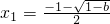
<-1,
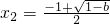
>-1,
所以此时f′(x)在(-1,x
2)上小于0,在(x
2,+∞)上大于0,即f(x)在(-1,+∞)上有唯一的极小值点
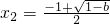
;
③当0<b<1时,在(-1,x
1),(x
2,+∞)上f′(x)>0,则(x
1,x
2)上f′(x)<0,
此时f(x)有一个极大值点
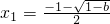
和一个极小值点
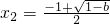
;
综上可知,b<0时,f(x)在(-1,+∞)上有唯一的极小值点
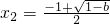
;
0<b<1时,f(x)有一个极大值点
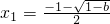
和一个极小值点
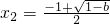
;
b≥1时,函数f(x)在(-1,+∞)上无极值点.
分析:(1)当b=-1时,f(0)=0,切线斜率kk=f′(0)=-1,点斜式即可求得切线方程;
(2)先求出函数的定义域,求导数f′(x),在定义域内按①当b≥1时,②当b<1时,③当0<b<1时三种情况解不等式f′(x)>0,f′(x)<0,根据极值点的定义即可求得;
点评:本题考查利用导数研究曲线上某点的切线方程、函数在某点取得极值的条件,注意f′(x
0)=0是x
0为可导数函数的极值点的必要不充分条件.

 ,
,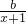 =
=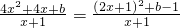 ,
,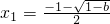 ,
,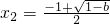 ,
,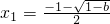 <-1,
<-1,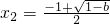 >-1,
>-1,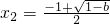 ;
;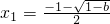 和一个极小值点
和一个极小值点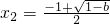 ;
;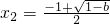 ;
;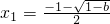 和一个极小值点
和一个极小值点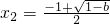 ;
;
