
| x | 2 | 3 | 4 | 5 | 6 |
| y | 22 | 38 | 55 | 65 | 70 |
分析 (Ⅰ)求出线性回归方程中的几何量,得到回归直线方程;
(Ⅱ)利用回归直线方程,直接求解即可.
解答 解:(Ⅰ)$\overline{x}=4,\overline{y}=50$,$b=\frac{{\sum_{i=1}^5{{x_i}{y_i}}}}{{\sum_{i=1}^5{x_i^2-5{{\overline x}^2}}}}=\frac{1123-5×4×5}{{90-5×{4^2}}}=12.3$,
$a=\bar y-bx=50-12.3×4=0.8$.
∴线性回归方程为:$\hat y=bx+a=12.3x+0.8$,
(Ⅱ)当x=10时,$\hat y=12.3×10+0.8=123.8$(万元),
即估计使用10年时维修费用是123.8(万元).
点评 本题考查回归直线方程的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}+\frac{2}{5}i$ | B. | $\frac{1}{5}-\frac{2}{5}i$ | C. | $-\frac{1}{5}-\frac{2}{5}i$ | D. | $\frac{1}{5}+\frac{2}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
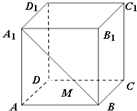 如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有( )| A. | ①② | B. | ①②③ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com