
分析 由同角三角函数基本关系可得sinα和sinβ,代入sin(α+β)=sinαcosβ+cosαsinβ,计算可得.
解答 解:∵$\frac{π}{6}$<α<$\frac{2π}{3}$,$\frac{π}{2}$<$\frac{π}{3}$+α<π,
又∵cos($\frac{π}{3}$+α)=-$\frac{3}{5}$
∴sin($\frac{π}{3}$+α)=$\frac{4}{5}$,
$0<β<\frac{π}{3}$,$\frac{2π}{3}$<$\frac{2π}{3}+β<π$,sin($\frac{2π}{3}+β$)=$\frac{5}{13}$,
∴cos($\frac{2π}{3}+β$)=-$\frac{12}{13}$,
sin(α+β)=-sin[π+(α+β)]=-sin[($\frac{π}{3}$+α)+($\frac{2π}{3}+β$)]
=-[sin($\frac{π}{3}$+α)cos($\frac{2π}{3}+β$)+sin($\frac{2π}{3}+β$)cos($\frac{π}{3}$+α)]=-[$\frac{4}{5}$×($-\frac{12}{13}$)-$\frac{3}{5}×\frac{5}{13}$]=$\frac{63}{65}$.
点评 本题考查两角和与差的正弦公式,涉及同角三角函数基本关系,属中档题.


科目:高中数学 来源: 题型:选择题
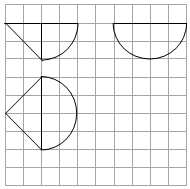 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | -25i | D. | 25i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com