
 -2x),1),B(1,
-2x),1),B(1, sin(π-2x)+a)(x∈R,a),y=
sin(π-2x)+a)(x∈R,a),y=
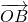 .
. ]时f(x)的最大值为4,求a的值.
]时f(x)的最大值为4,求a的值. -2x),1),B(1,
-2x),1),B(1, sin(π-2x)+a)(a、x∈R,),
sin(π-2x)+a)(a、x∈R,),
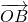 =(1+sin(
=(1+sin( -2x),1)•(1,
-2x),1)•(1, sin(π-2x)+a)=1+cos2x+
sin(π-2x)+a)=1+cos2x+ sin2x+a=2sin(
sin2x+a=2sin( +2x)+a+1
+2x)+a+1  ]时,
]时, ≤2x+
≤2x+ ≤
≤ ,故当2x+
,故当2x+ =
= 时,函数y有最大值等于2+a+1=4,a=1.
时,函数y有最大值等于2+a+1=4,a=1. +2x)+a+1.
+2x)+a+1. 的范围,从而求出f(x)=2sin(
的范围,从而求出f(x)=2sin( +2x)+a+1的最大值,再根据它的最大值等于4求出a的值
+2x)+a+1的最大值,再根据它的最大值等于4求出a的值

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| 3 |
| OA |
| OB |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2008年广东省广州市海珠区高考数学一模试卷(文科)(解析版) 题型:解答题
 -2x),1),B(1,
-2x),1),B(1, sin(π-2x)+a)(x∈R,a),y=
sin(π-2x)+a)(x∈R,a),y=
 .
. ]时f(x)的最大值为4,求a的值.
]时f(x)的最大值为4,求a的值.查看答案和解析>>
科目:高中数学 来源:海珠区一模 题型:解答题
| π |
| 2 |
| 3 |
| OA |
| OB |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com