

| A. | -$\frac{\sqrt{5}}{5}$ | B. | -1 | C. | -$\frac{2\sqrt{13}}{13}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 建立如图所示平面直角坐标系,求出A、D、B的坐标,得到$\overrightarrow{AB}、\overrightarrow{AD}$的坐标,代入投影公式求解.
解答 解:建立如图所示平面直角坐标系,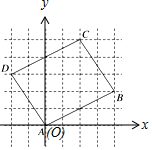
则A(0,0),B(4,2),D(-2,3).
∴$\overrightarrow{AB}=(4,2)$,$\overrightarrow{AD}=(-2,3)$.
∴$\overrightarrow{AB}•\overrightarrow{AD}=-8+6=-2$,$|\overrightarrow{AB}|=\sqrt{{4}^{2}+{2}^{2}}=2\sqrt{5}$.
∴向量$\overrightarrow{AD}$在$\overrightarrow{AB}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}|}=\frac{-2}{2\sqrt{5}}=-\frac{\sqrt{5}}{5}$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上投影的概念,是中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | m | $\frac{1}{4}$ | $\frac{1}{6}$ |
| A. | $\frac{7}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 不优秀 | 合计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 合计 | 17 | 73 | 90 |
| A. | 0.3~0.4 | B. | 0.4~0.5 | C. | 0.5~0.6 | D. | 0.6~0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 将大小形状相同的3个黄球和5个黑球放入如图所示的2×5的十宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),如果同色球不加以区分,则所有不同的放法种数为( )
将大小形状相同的3个黄球和5个黑球放入如图所示的2×5的十宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),如果同色球不加以区分,则所有不同的放法种数为( )| A. | 40 | B. | 36 | C. | 24 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow 0$ | B. | $\overrightarrow a=\overrightarrow b$ | ||
| C. | $\overrightarrow a$与$\overrightarrow b$共线反向 | D. | 存在正实数λ,使$\overrightarrow a=λ\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com