
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意,依次分析题目所给的关系式,对于①、利用元素与集合的关系分析;对于②、结合空集的性质分析; 对于③、由集合的定义与表示方分析,对于④、⑤,结合补集的定义、性质分析,可得其是否正确,即可得答案.
解答 解:根据题意,依次分析所给的关系:
对于①、0是集合{0}的元素,即0∈{0},故①正确;
对于②、空集∅是任何集合的子集,即有∅⊆{0},即②正确;
对于③、集合{0,1}中有2个元素:0与1,而集合{(0,1)}为点集,只有元素(0,1),两者不相等,故③错误;
对于④、由补集的性质,可得∁U(A∪B)=(∁UA)∩(∁UB),故④错误;
对于⑤、∁UA表示全集U中除集合A之外全部元素组成的集合,则有(∁UA)∩A=∅,故⑤正确;
共有3个正确的关系;
故选:C.
点评 本题考查集合与元素之间的关系以及集合间的关系,是对基础概念的考查,关键正确掌握集合的概念以及表示方法.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
| 年龄(岁) | 频率 | |
| 第1组 | [25,30) | 0.1 |
| 第2组 | [30,35) | 0.1 |
| 第3组 | [35,40) | 0.4 |
| 第4组 | [40,45) | 0.3 |
| 第5组 | [45,50] | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
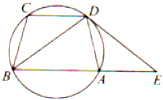 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 1007 | D. | 1008 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com