
 中,已知
中,已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆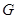 与抛物线
与抛物线 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
. 的方程;
的方程; 与椭圆
与椭圆 相交于
相交于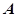 、
、 两点,若
两点,若 (
( 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. (Ⅱ) 直线
(Ⅱ) 直线 与圆
与圆 相切
相切 ,又
,又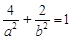 ,结合
,结合 ,可解得
,可解得 的值,从而得椭圆的标准方程.(Ⅱ)设
的值,从而得椭圆的标准方程.(Ⅱ)设 ,则
,则 ,当直线与
,当直线与 轴垂直时,由椭圆的对称性易求
轴垂直时,由椭圆的对称性易求 两点的坐标,并判断直线
两点的坐标,并判断直线 与圆
与圆 是否相切.当直线
是否相切.当直线 的不与
的不与 轴垂直时,可设其方程为
轴垂直时,可设其方程为 ,与椭圆方程联立方程组
,与椭圆方程联立方程组 消法
消法 得:
得: ,
, ,结合
,结合 ,可得
,可得 与
与 的关系,由此可以判断与该直线与圆
的关系,由此可以判断与该直线与圆 的位置关系.
的位置关系. ,又
,又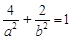 , 2分
, 2分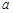 可得,
可得, ,解得
,解得 或
或 (舍去),则
(舍去),则 ,
, 的方程为
的方程为 . 4分
. 4分 与圆
与圆 相切.
相切. 不过坐标原点,设
不过坐标原点,设 的坐标分别为
的坐标分别为
 轴时,直线
轴时,直线 的方程为
的方程为 且
且
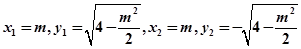


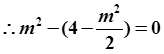
 ,故直线
,故直线 的方程为
的方程为 ,
, 到直线
到直线 的距离为
的距离为 ,又圆
,又圆 的圆心为
的圆心为 ,
, 所以直线
所以直线 与圆
与圆 相切 7分
相切 7分 不垂直于
不垂直于 轴时,
轴时, 的方程为
的方程为 ,联立直线和椭圆方程消去
,联立直线和椭圆方程消去 得;
得; ,
,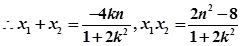



 ,故
,故 ,
, ① 10分
① 10分 的圆心为
的圆心为 ,半径
,半径 ,
, 到直线
到直线 的距离为
的距离为 ,
, ② 将①式带入②式得:
② 将①式带入②式得: ,
,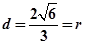 因此,直线
因此,直线 与圆
与圆 相切 13分
相切 13分

科目:高中数学 来源:不详 题型:解答题
 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,右焦点到直线
,右焦点到直线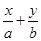 =1的距离d=
=1的距离d=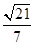 ,O为坐标原点.
,O为坐标原点.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (
( >b>0)的离心率e=
>b>0)的离心率e=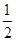 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( ) 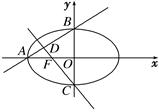
 B.
B.
 D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
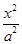 +
+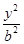 =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )A. + + =1 =1 | B. + + =1 =1 | C. + + =1 =1 | D. + + =1 =1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com