
【题目】已知函数![]() .
.
(1)判断f(x)的奇偶性,说明理由;
(2)当x>0时,判断f(x)的单调性并加以证明;
(3)若f(2t)-mf(t)>0对于t∈(0,+∞)恒成立,求m的取值范围.
【答案】(1)偶函数,理由见解析;(2)在![]() 上是增函数,证明见解析;(3)
上是增函数,证明见解析;(3)![]() .
.
【解析】
(1)利用![]() 与
与![]() 的关系,结合定义域判断奇偶性,即可得出答案.(2)换元法,转化成对勾函数,结合对勾函数性质,即可.(3)代入
的关系,结合定义域判断奇偶性,即可得出答案.(2)换元法,转化成对勾函数,结合对勾函数性质,即可.(3)代入![]() 的解析式,建立关于s的新函数,结合该函数单调性,计算最值,即可得出答案。
的解析式,建立关于s的新函数,结合该函数单调性,计算最值,即可得出答案。
(1)∵函数f(x)=3x+![]() ,定义域R,关于原点对称,
,定义域R,关于原点对称,
且对一切x∈R,都有f(-x)=3-x+![]() =
=![]() +3x=f(x)成立,
+3x=f(x)成立,
∴f(x)是偶函数.
综上所述:f(x)是偶函数.
(2)函数f(x)=3x+![]() 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
令3x=t,当x>0时,t>30=1,则y=g(t)=t+![]() ,
,
设1<t1<t2,
g(t1)-g(t2)=(t1+![]() )-(t2+
)-(t2+![]() )=(t1t2-1)
)=(t1t2-1)![]() ,
,
又由a∈(0,![]() )且1<t1<t2,
)且1<t1<t2,
则![]() <0,t1t2-1>0,
<0,t1t2-1>0,
则g(t1)-g(t2)<0,
函数y=t+![]() 在t∈(1,+∞)上是增函数,
在t∈(1,+∞)上是增函数,
即函数f(x)在(0,+∞)上为增函数.
(3)∵函数f(x)=3x+![]() ,
,
∴f(2t)-mf(t)>0对于t∈(0,+∞)恒成立,
等价于:m(3t+![]() )<32t+
)<32t+![]() 对于t∈(0,+∞)恒成立,
对于t∈(0,+∞)恒成立,
即m(3t+![]() )<(3t+
)<(3t+![]() )2-2对于t∈(0,+∞)恒成立,
)2-2对于t∈(0,+∞)恒成立,
∵3t+![]() >0,∴m<3t+
>0,∴m<3t+![]() -
-![]() 对于t∈(0,+∞)恒成立,
对于t∈(0,+∞)恒成立,
令3t+![]() =s,∵t∈(0,+∞),
=s,∵t∈(0,+∞),
∴由(2)知:s>2,则m<s-![]() 对于s∈(2,+∞)恒成立,
对于s∈(2,+∞)恒成立,
记y=s-![]() ,在s∈(2,+∞)上是增函数,
,在s∈(2,+∞)上是增函数,
∴y>2-![]() =1,
=1,
∴m≤1
即m的取值范围为(-∞,1],
综上所述:m的取值范围是(-∞,1].


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() ,侧面
,侧面![]() 是边长为
是边长为![]() 的正三角形,侧面
的正三角形,侧面![]() 底面
底面![]() .
.
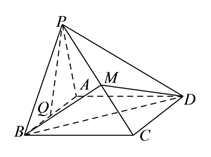
(![]() )设
)设![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(![]() )求斜线
)求斜线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(![]() )在侧棱
)在侧棱![]() 上存在一点
上存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56
B.60
C.120
D.140
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是 ![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是 ![]() ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(1)“星队”至少猜对3个成语的概率;
(2)“星队”两轮得分之和为X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足:①对于任意实数x,y都有f(x+y)+1=f(x)+f(x)且f(![]() )=0;②当x>
)=0;②当x>![]() 时,f(x)<0.
时,f(x)<0.
(1)求证:f(x)=![]() +
+![]() f(2x);
f(2x);
(2)用数学归纳法证明:当x∈[![]() ,
,![]() ](n∈N*)时, f(x)≤1-
](n∈N*)时, f(x)≤1-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-x2+2ax.
(1)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)在R上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知五面体![]() ,其中
,其中![]() 内接于圆
内接于圆![]() ,
,![]() 是圆
是圆![]() 的直径,四边形
的直径,四边形![]() 为平行四边形,且
为平行四边形,且![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,且二面角
,且二面角![]() 所成角
所成角![]() 的余弦值为
的余弦值为![]() ,试求该几何体
,试求该几何体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com