
【题目】如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() ,侧面
,侧面![]() 是边长为
是边长为![]() 的正三角形,侧面
的正三角形,侧面![]() 底面
底面![]() .
.
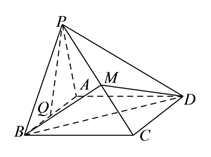
(![]() )设
)设![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(![]() )求斜线
)求斜线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(![]() )在侧棱
)在侧棱![]() 上存在一点
上存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )
)![]() .
.
【解析】试题分析:(I)由Q为侧面正三角形PAB的边AB的中点,可得PQ⊥AB,再利用面面垂直的性质定理即可证明线面垂直;(II)通过结论空间直角坐标系,利用斜线的方向向量和平面的法向量的夹角即可得出;(III)利用两个平面的法向量的夹角即可得到二面角,进而解出.
解析:
(![]() )证明:∵侧面
)证明:∵侧面![]() 是正三角形,
是正三角形,![]() 中点为
中点为![]() ,
,
∴![]() ,
,
∵侧面![]() 底面
底面![]() ,
,
侧面![]() 底面
底面![]() ,
,
![]() 侧面
侧面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )连接
)连接![]() ,设
,设![]() 点,
点,
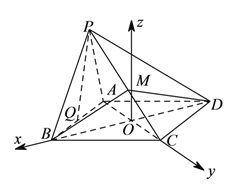
以![]() 为原点,
为原点,![]() ,
,![]() 过
过![]() 点且垂直于平面
点且垂直于平面![]() 的直线分别为
的直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
设斜线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则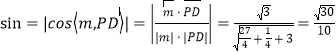 .
.
(![]() )设
)设![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
∴![]() ,
,![]() ,
,
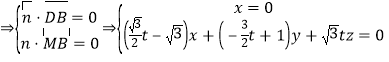 ,
,
取![]() ,
,![]() ,
,
又∵平面![]() 的法向量
的法向量![]() ,
,
∴![]() ,
,
∴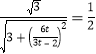 ,
,
解出![]() (舍去)或
(舍去)或![]() ,
,
此时![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是![]() 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是![]() .假设各局比赛结果相互独立.
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民用水拟实行阶梯水价,每人月用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如图频率分布直方图:
(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个顶点为A(﹣3,0),B(2,1),C(﹣2,3),求:
(1)BC所在直线的方程;
(2)BC边上中线AD所在直线的方程;
(3)BC边上的垂直平分线DE的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3-3(a+1)x2+6ax+8,其中a∈R.已知f(x)在x=3处取得极值.
(1)求f(x)的解析式; (2)求f(x)在点A(1,16)处的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.
AD.
(1)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(2)证明:平面PAB⊥平面PBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断f(x)的奇偶性,说明理由;
(2)当x>0时,判断f(x)的单调性并加以证明;
(3)若f(2t)-mf(t)>0对于t∈(0,+∞)恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com