
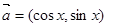 ,
,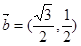 ,函数
,函数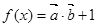 。
。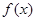 的值域和函数的单调递增区间;
的值域和函数的单调递增区间; 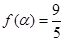 ,且
,且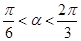 时,求
时,求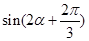 的值.
的值. ;单调增区间为
;单调增区间为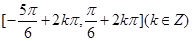 ;(Ⅱ)
;(Ⅱ)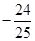 .
.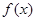 的特点,利用平面向量的数量积的运算法则化简,然后利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,从而确定出
的特点,利用平面向量的数量积的运算法则化简,然后利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,从而确定出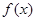 的解析式,
的解析式,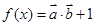 、数量积公式和三角函数恒等变换,求出
、数量积公式和三角函数恒等变换,求出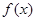
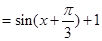 ,在根据正弦函数的性质求出函数
,在根据正弦函数的性质求出函数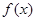 的值域;
的值域;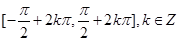 ,列出不等式,求出不等式的解集即可得到
,列出不等式,求出不等式的解集即可得到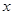 的取值范围即为
的取值范围即为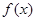 的递增区间;
的递增区间;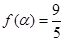 ,代入
,代入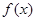 的解析式中,得到
的解析式中,得到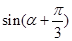 的值,根据
的值,根据 的范围求出
的范围求出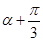 的范围,利用同角三角函数间的基本关系求出
的范围,利用同角三角函数间的基本关系求出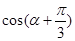 的值,把所求的式子利用二倍角的正弦函数公式化简,将
的值,把所求的式子利用二倍角的正弦函数公式化简,将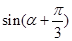 和
和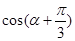 的值代入即可求出值.
的值代入即可求出值.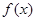

 (2分)
(2分)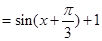 (4分)
(4分)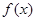 的值域是
的值域是 ; (5分)
; (5分)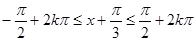 ,解得
,解得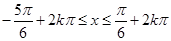 (7分)
(7分)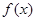 的单调增区间为
的单调增区间为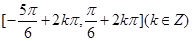 . (8分)
. (8分)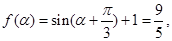 得
得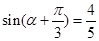 ,
,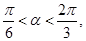 所以
所以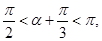 得
得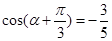 , (10分)
, (10分)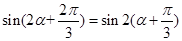
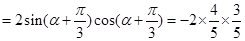
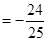 (12分).
(12分).

科目:高中数学 来源:不详 题型:解答题
 .
. 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);| | | | | | |
| | | | | | |
| | | | | | |

 的单调递增区间;
的单调递增区间; 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的周期为
的周期为 .
.
 ,求它的振幅、初相;
,求它的振幅、初相;  的图像;
的图像; 时,根据实数
时,根据实数 的不同取值,讨论函数
的不同取值,讨论函数 的零点个数.
的零点个数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (
( ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是 ,
, 的解析式及其单调增区间;
的解析式及其单调增区间; ,且
,且 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当 时,试求函数
时,试求函数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. 的单调递减区间;
的单调递减区间; 的图像向左平移
的图像向左平移 个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图像横坐标变为原来的2倍(纵坐标不变)后得到 的图像,若
的图像,若 的图像与直线
的图像与直线 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是 求数列
求数列 的前2n项的和。
的前2n项的和。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ”的( ).
”的( ).| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
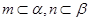 ,
,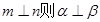 ;
; 是周期为2
是周期为2 的偶函数;
的偶函数; 的焦点为F,点P为抛物线上任意一点,则
的焦点为F,点P为抛物线上任意一点,则 的最小值为2;
的最小值为2;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com