
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.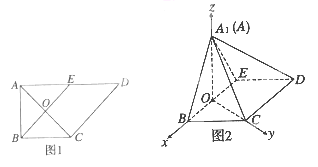
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
【答案】
(1)
见解析。
(2)
a=6
【解析】(I)在图1中,∵AB=BC=1,AD=2,E是AD的中点,∠BAD= π 2 , ∴BE⊥AC,
即在图2中,BE⊥OA1 , BE⊥OC,则BE⊥平面A1OC;∵CD∥BE,∴CD⊥平面A1OC;
(II)由已知,平面A1BE⊥平面BCDE,
且平面A1BE![]() 平面BCDE=BE
平面BCDE=BE
又由(I)知,A1O⊥BE,所以
A1O⊥平面BCDE,
即A1O是四棱锥A1-BCDE的高,
由图1可知,A1O=![]() AB=
AB=![]() a,平行四边形BCDE面积S=BC-AB=a2 ,
a,平行四边形BCDE面积S=BC-AB=a2 ,
从而四棱锥A1-BCDE的为
v=![]() xSxA1O=
xSxA1O=![]() xa2x
xa2x![]() a=
a=![]() a3 ,
a3 ,
由![]() a3=36
a3=36![]() ,得a=6.
,得a=6.
【考点精析】解答此题的关键在于理解向量语言表述线面的垂直、平行关系的相关知识,掌握要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若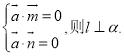 .
.


科目:高中数学 来源: 题型:
【题目】(2015![]() 全国统考II)设函数f(x)=ln(1+|x|)-
全国统考II)设函数f(x)=ln(1+|x|)-![]() ,则使得f(x)
,则使得f(x)![]() f(2x-1)成立的x的取值范围是()
f(2x-1)成立的x的取值范围是()
A.(![]() ,1)
,1)
B.(-![]() ,
,![]() )
)![]() (1,+
(1,+![]() )
)
C.(-![]() ,
,![]() )
)
D.(-![]() ,-
,-![]() )
)![]() (
(![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
A.16
B.18
C.25
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,A , B , C , D为平面四边形ABCD的四个内角.
(1)证明:tan![]() =
=![]()
(2)若A+C=180°, AB=6, BC=3, CD=4, AD=5, 求tan![]() +tan
+tan![]() +tan
+tan![]() +tan
+tan![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.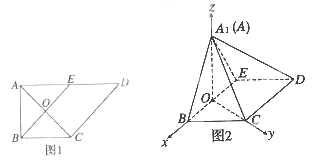
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com