
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.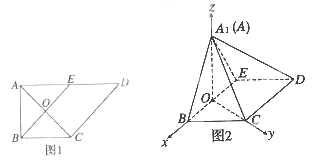
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
【答案】
(1)
见解析。
(2)
a=6
【解析】(I)在图1中,∵AB=BC=1,AD=2,E是AD的中点,∠BAD= π 2 , ∴BE⊥AC,
即在图2中,BE⊥OA1 , BE⊥OC,则BE⊥平面A1OC;∵CD∥BE,∴CD⊥平面A1OC;
(II)由已知,平面A1BE⊥平面BCDE,
且平面A1BE![]() 平面BCDE=BE
平面BCDE=BE
又由(I)知,A1O⊥BE,所以
A1O⊥平面BCDE,
即A1O是四棱锥A1-BCDE的高,
由图1可知,A1O=![]() AB=
AB=![]() a,平行四边形BCDE面积S=BC-AB=a2 ,
a,平行四边形BCDE面积S=BC-AB=a2 ,
从而四棱锥A1-BCDE的为
v=![]() xSxA1O=
xSxA1O=![]() xa2x
xa2x![]() a=
a=![]() a3 ,
a3 ,
由![]() a3=36
a3=36![]() ,得a=6.
,得a=6.
【考点精析】解答此题的关键在于理解向量语言表述线面的垂直、平行关系的相关知识,掌握要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若 .
.


科目:高中数学 来源: 题型:
【题目】对于非空实数集A,定义![]() 对任意
对任意![]() .设非空实数集
.设非空实数集![]() .现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有
.现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有![]() ;(2)对于任意给定符合题设条件的集合C,D,必有
;(2)对于任意给定符合题设条件的集合C,D,必有![]() ;(3)对于任意给定符合题设条件的集合C,D,必有
;(3)对于任意给定符合题设条件的集合C,D,必有![]() ;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的
;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的![]() ,恒有
,恒有![]() .以上命题正确的个数是( )
.以上命题正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1 , P2 , P3 , P4 , P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(1)(I)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
乘客 | P1 | P2 | P3 | P4 | P5 |
座位号 | 3 | 2 | 1 | 4 | 5 |
3 | 2 | 4 | 5 | 1 | |
(2)(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P1坐到5号座位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.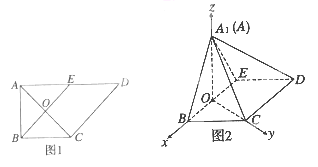
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A , B两点,线段AB的垂直平分线分别交直线l和AB于 点P , C , 若PC=2AB , 求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点。
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线AC1与平面AA1BB1所成的角为45°,求三棱锥F-AEC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加. 现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设![]() 为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件
为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件![]() 发生的概率
发生的概率
(2)设![]() 为选出的4人中种子选手的人数,求随机变量
为选出的4人中种子选手的人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com