
【题目】对于非空实数集A,定义![]() 对任意
对任意![]() .设非空实数集
.设非空实数集![]() .现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有
.现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有![]() ;(2)对于任意给定符合题设条件的集合C,D,必有
;(2)对于任意给定符合题设条件的集合C,D,必有![]() ;(3)对于任意给定符合题设条件的集合C,D,必有
;(3)对于任意给定符合题设条件的集合C,D,必有![]() ;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的
;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的![]() ,恒有
,恒有![]() .以上命题正确的个数是( )
.以上命题正确的个数是( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ﹣2cosθ﹣6sinθ+ ![]() =0,直线l的参数方程为
=0,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,点P的坐标为(3,3),求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 全国统考II)设函数f(x)=ln(1+|x|)-
全国统考II)设函数f(x)=ln(1+|x|)-![]() ,则使得f(x)
,则使得f(x)![]() f(2x-1)成立的x的取值范围是()
f(2x-1)成立的x的取值范围是()
A.(![]() ,1)
,1)
B.(-![]() ,
,![]() )
)![]() (1,+
(1,+![]() )
)
C.(-![]() ,
,![]() )
)
D.(-![]() ,-
,-![]() )
)![]() (
(![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、C1D1上,A1E=D1F=4,过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E、F分别在A1B1、C1D1上,A1E=D1F=4,过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。
(1)(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(2)(Ⅱ)求直线AF与平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.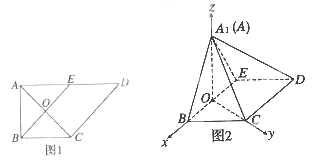
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com