
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
【答案】
(1)
(0.0) (![]() ,
,![]() )
)
(2)
4
【解析】(1)曲线C2的直角坐标方程为x2+y2-2y=0,曲线C3 的直角坐标方程分别为x2+y2-2![]() x=0,联立两方程组解可得
x=0,联立两方程组解可得![]() 或
或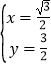 , 所以C2与C3得交点直角坐标为(0.0) (
, 所以C2与C3得交点直角坐标为(0.0) (![]() ,
,![]() )。
)。
(2)曲线C1极坐标方程为![]() =
=![]() (
(![]()
![]() R,
R,![]() ≠0),其中0
≠0),其中0![]()
![]()
![]() , 因此点A的极坐标为(2sin
, 因此点A的极坐标为(2sin![]() ,
, ![]() ),点B的极坐标为 (2
),点B的极坐标为 (2![]() cos
cos![]() ,
, ![]() ),所以|AB|=|2sin
),所以|AB|=|2sin![]() -2
-2![]() cos
cos![]() |=4|sin(
|=4|sin(![]() -
-![]() )|,当
)|,当![]() =
=![]() 时,|AB|取得最大值,最大值为4。
时,|AB|取得最大值,最大值为4。
【考点精析】根据题目的已知条件,利用参数方程的定义的相关知识可以得到问题的答案,需要掌握在平面直角坐标系中,如果曲线上任意一点的坐标![]() 都是某个变数
都是某个变数![]() 的函数
的函数![]() 并且对于
并且对于![]() 的每一个允许值,由这个方程所确定的点
的每一个允许值,由这个方程所确定的点![]() 都在这条曲线上,那么这个方程就叫做这条曲线的参数方程.
都在这条曲线上,那么这个方程就叫做这条曲线的参数方程.


科目:高中数学 来源: 题型:
【题目】如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆. 
(1)若围墙AP、AQ总长度为200米,如何可使得三角形地块APQ面积最大?
(2)已知竹篱笆长为 ![]() 米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
(1)求椭圆C的方程;
(2)是否存在直线l,使得点N平分线段A1B1?若存在,求求出直线l的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“若![]() ,则关于x的不等式
,则关于x的不等式![]() 的解集为空集”,那么它的逆命题,否命题,逆否命题,以及原命题中,假命题的个数是( )
的解集为空集”,那么它的逆命题,否命题,逆否命题,以及原命题中,假命题的个数是( )
A.0B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于非空实数集A,定义![]() 对任意
对任意![]() .设非空实数集
.设非空实数集![]() .现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有
.现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有![]() ;(2)对于任意给定符合题设条件的集合C,D,必有
;(2)对于任意给定符合题设条件的集合C,D,必有![]() ;(3)对于任意给定符合题设条件的集合C,D,必有
;(3)对于任意给定符合题设条件的集合C,D,必有![]() ;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的
;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的![]() ,恒有
,恒有![]() .以上命题正确的个数是( )
.以上命题正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一周期内的图像时,列表并填入的部分数据如下表:
在某一周期内的图像时,列表并填入的部分数据如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)请写出上表的![]() 及函数
及函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像上各点的横坐标缩小为原来的
个单位,再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的解析式及
的解析式及 的单调递增区间;
的单调递增区间;
(3)在(2)的条件下,若![]() 在
在![]() 上恰有奇数个零点,求实数
上恰有奇数个零点,求实数![]() 与零点个数
与零点个数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图,根据统计图:

(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,60]间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎?并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=4y 的焦点F也是椭圆c2:![]() 的一个焦点, C1和C2的公共弦长为
的一个焦点, C1和C2的公共弦长为![]()
(1)求 C2的方程;
(2)过点F 的直线 l与 C1相交于A与B两点, 与C2相交于C , D两点,且![]() 与
与![]() 同向
同向
(ⅰ)若 ![]() 求直线l的斜率;
求直线l的斜率;
(ⅱ)设 C1在点 A处的切线与 x轴的交点为M ,证明:直线l 绕点 F旋转时, ![]() MFD总是钝角三角形。
MFD总是钝角三角形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A , B两点,线段AB的垂直平分线分别交直线l和AB于 点P , C , 若PC=2AB , 求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com