
【题目】已知抛物线C1:x2=4y 的焦点F也是椭圆c2:![]() 的一个焦点, C1和C2的公共弦长为
的一个焦点, C1和C2的公共弦长为![]()
(1)求 C2的方程;
(2)过点F 的直线 l与 C1相交于A与B两点, 与C2相交于C , D两点,且![]() 与
与![]() 同向
同向
(ⅰ)若 ![]() 求直线l的斜率;
求直线l的斜率;
(ⅱ)设 C1在点 A处的切线与 x轴的交点为M ,证明:直线l 绕点 F旋转时, ![]() MFD总是钝角三角形。
MFD总是钝角三角形。
【答案】(1)![]()
(2)(i)![]() ,
,
(ii)见解析。
【解析】(1)根据已知条件可求得C2的焦点坐标为(0,1),再利用公共弦长为![]() 即可求解由C1:
即可求解由C1:![]() 知其焦点F的坐标(0,1)因为F也是椭圆C2的一焦点,所以
知其焦点F的坐标(0,1)因为F也是椭圆C2的一焦点,所以![]() ①又C1与C2的公共弦长为
①又C1与C2的公共弦长为![]() , C1与C2都关于y轴对称,且C1的方程为
, C1与C2都关于y轴对称,且C1的方程为![]() 由此易得C1与C2公共点的坐标为
由此易得C1与C2公共点的坐标为![]() 所以,
所以,![]() ②联立①,②得a2=9,b2=8故C2的方程为
②联立①,②得a2=9,b2=8故C2的方程为![]()
(2)(ⅰ)设直线l的斜率为k,则l的方程为y=kx+1,由![]() 得x2+16kx+64=0,根据条件可知
得x2+16kx+64=0,根据条件可知![]() , 从而可以建立关于k的方程,即可求解,如图f
, 从而可以建立关于k的方程,即可求解,如图f![]() 因为
因为![]() 与
与![]() 同向且
同向且![]() 所以
所以![]() , 从而
, 从而![]() ,于是
,于是![]() ③,设直线l的斜率为k,则l的方程为y=kx+1,由
③,设直线l的斜率为k,则l的方程为y=kx+1,由![]() 得
得![]() 而x1x2是这个方程的两个根所以
而x1x2是这个方程的两个根所以![]() 由
由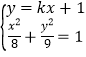 得(9+8k)2+16kx-64=0而x3x4是这个方程的两个根,所以
得(9+8k)2+16kx-64=0而x3x4是这个方程的两个根,所以![]()
![]() ⑤将④⑤带入③得
⑤将④⑤带入③得![]() , 即
, 即![]() , 所以
, 所以![]() , 解得,k=
, 解得,k=![]()
(ⅱ)根据条件可说明![]() , 因此
, 因此![]() 是锐角,从而
是锐角,从而![]() 是钝角,即可得证由
是钝角,即可得证由![]() 令y=0得
令y=0得![]() 即
即![]() 所以,
所以,![]() 而
而![]() 于是
于是![]() 因此
因此![]() 是锐角。
是锐角。
【考点精析】根据题目的已知条件,利用椭圆的标准方程和椭圆的参数方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ;椭圆
;椭圆![]()
![]() 的参数方程可表示为
的参数方程可表示为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx﹣ ![]() cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)如图,四边形ABCD为菱形,∠ABC=120°,E , F是平面ABCD同一侧的两点,BE⊥平面ABCD , DF⊥平面ABCD , BE=2DF , AE⊥EC.
(1)证明:平面AEC⊥平面AFC
(2)求直线AE与直线CF所成角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=2x , g(x)=x2+ax(其中a![]() R).对于不相等的实数x1, x2 , 设m=
R).对于不相等的实数x1, x2 , 设m=![]() ,n=
,n=![]() .
.
现有如下命题:
(1)对于任意不相等的实数x1, x2 , 都有m>0;
(2)对于任意的a及任意不相等的实数x1, x2 , ,都有n>0;
(3)对于任意的a , 存在不相等的实数x1, x2 , 使得m=n;
(4)对于任意的a , 存在不相等的实数x1, x2 , 使得m=-n.
其中的真命题有 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
A.16
B.18
C.25
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)设![]() . 若p:
. 若p:![]() 成等比数列;
成等比数列;
q:![]() ,则( )
,则( )
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com