
【题目】在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ﹣2cosθ﹣6sinθ+ ![]() =0,直线l的参数方程为
=0,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,点P的坐标为(3,3),求|PA|+|PB|的值.
【答案】
(1)解:曲线C的极坐标方程为ρ﹣2cosθ﹣6sinθ+ ![]() =0,
=0,
可得:ρ2﹣2ρcosθ﹣6ρsinθ+1=0,
可得x2+y2﹣2x﹣6y+1=0,
曲线C的普通方程:x2+y2﹣2x﹣6y+1=0
(2)解:由于直线l的参数方程为 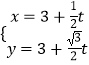 (t为参数).
(t为参数).
把它代入圆的方程整理得 t2+2t﹣5=0,∴t1+t2=﹣2,t1t2=﹣5,
|PA|=|t1|,|PB|=|t2|,|PA|+|PB|=|t1|+|t2|= ![]() =2
=2 ![]() .
.
∴|PA|+|PB|的值2 ![]()
【解析】(1)利用极坐标与直角坐标化简公式化简求解即可.(2)把直线方程代入圆的方程化简可得t的二次方程,利用根与系数的关系,以及|PA|=|t1|,|PB|=|t2|求出|PA||PB|.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船.在
处有一艘走私船.在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方缉私船奉命以
处的我方缉私船奉命以![]() 海里
海里![]() 小时的速度追截走私船,此时走私船正以
小时的速度追截走私船,此时走私船正以![]() 海里
海里![]() 小时的速度从
小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知曲线C1的参数方程为 ![]() ,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
(Ⅰ)求C1的极坐标方程与C2的直角坐标方程;
(Ⅱ)若P是C1上任意一点,过点P的直线l交C2于点M,N,求|PM||PN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
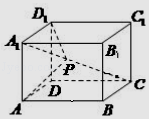
【题目】如图,在长方体ABCD﹣A1B1C1D1中, ![]() ,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当
,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当 ![]() 时,D1P∥平面BDC1;
时,D1P∥平面BDC1;
②当 ![]() 时,A1C⊥平面D1AP;
时,A1C⊥平面D1AP;
③当∠APD1的最大值为90°;
④AP+PD1的最小值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=4cosθ,以极点为坐标原点,极轴为x轴的非负半轴建立平面直角坐标系,直线l经过点M(5,6),且斜率为 ![]() .
.
(1)求圆 C的平面直角坐标方程和直线l的参数方程;
(2)若直线l与圆C交于A,B两点,求|MA|+|MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆. 
(1)若围墙AP、AQ总长度为200米,如何可使得三角形地块APQ面积最大?
(2)已知竹篱笆长为 ![]() 米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
米,AP段围墙高1米,AQ段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+be﹣x﹣2asinx(a,b∈R).
(1)当a=0时,讨论函数f(x)的单调区间;
(2)当b=﹣1时,若f(x)>0对任意x∈(0,π)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于非空实数集A,定义![]() 对任意
对任意![]() .设非空实数集
.设非空实数集![]() .现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有
.现给出以下命题:(1)对于任意给定符合题设条件的集合C,D,必有![]() ;(2)对于任意给定符合题设条件的集合C,D,必有
;(2)对于任意给定符合题设条件的集合C,D,必有![]() ;(3)对于任意给定符合题设条件的集合C,D,必有
;(3)对于任意给定符合题设条件的集合C,D,必有![]() ;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的
;(4)对于任意给定符合题设条件的集合C,D,必存在常数a,使得对任意的![]() ,恒有
,恒有![]() .以上命题正确的个数是( )
.以上命题正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com